Important properties of z-transforms
The proofs can be easily obtained by using basic z-transform definition and transformations in summation.
(1) Linearity If ?[x(n)] = X(z) with the ROC rx1 <|z|< rx2 and ?[y(n)] z2 + 2z , ROC: the whole- = Y(z) with ROC ry1 <|z|< ry2 then ?[a x(n) + b y(n)] = a X(z) + b Y(z) with ROC at least the overlap of the ROC's of Y(z) and X(z) and if there is any pole-zero cancellation because of linear combination, then the ROC can be larger.
(2) Translation (Time-shifting)
If ?[x(n)] = X(z) with ROC r1<|z|< r2 then ?[x(n-k)] = z-k X(z) with same ROC except for the possible deletion or addition of z = 0 or z = ∞ because of z-k.
(3) Multiplication by the complex exponential sequence
If ?[x(n)] = 
X(z) with ROC r1 <|z|< r2 then ?[an x(n)] = X ( z) z→( z / a ) with ROC |a| r1 <|z|< |a| r2.
Example
Given x(n) = {1, 2} and x2(n) = 0.5n x(n-2) find X(z) and X2(z) and their ROCs respectively.
(4) Multiplication by a ramp If ?[x(n)] = X(z) with ROC r1 <|z|< r2 then
?[n x(n)] = - z dX ( z)/dz with ROC r1 <|z|< r2.
Example Given x(n) = {1, 2} and x2(n) = (1+ n + n 2 ) x(n) find X(z) and X2(z) and their ROCs respectively. ?[x2(n)] = ?[1] + ?[n x(n)] + ?[n [n x(n)]] = ...
(5) Time reversal If ?[x(n)] = X(z) with ROC r1 <|z|< r2 then ?[ x(-n)] = X (z -1 ) having ROC (1/ r2 )<|z|< (1/ r1 )
Example Given x(n) = 2- n u(n) and X2 ( z) = z X ( z -1 ) evaluate x2(n).
x(n) = (0.5)n u(n) , X(z) = z/z - 0.5 , ROC: 0.5 <|z|
?-1{ X ( z -1 ) } = x(-n); x2(n) = ?-1{ z X ( z -1 ) } = x(-(n+1)).= 2-( -( n+1)) u(-(n + 1))
(6) Convolution in the time domain leads to multiplication in frequency domain
Given ?[x(n)] =
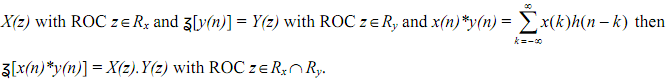
(7) Multiplication in the time domain leads to convolution in frequency domain
If ?[x(n)] = X(z)
having ROC rx1 <|z|< rx2 and ?[y(n)] = Y(z) with ROC ry1 <|z|< ry2 then
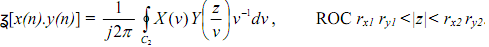
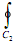is a complex contour integral and C2 is a closed contour in intersection of the ROCs of X(v) and Y(z/v).
(8) Initial Value Theorem If x(n) is causal sequence with z transform X(z), then
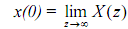
(9) Final Value Theorem If ?[x(n)] = X(z) and poles of X(z) are all in the unit circle then value of x(n) as n→∞ can be given by
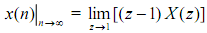
some also give this as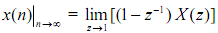 
Email based Important properties of z-transforms assignment help - Important properties of z-transforms homework help at Expertsmind
Are you finding answers for Important properties of z-transforms based questions? Ask Important properties of z-transforms questions and get answers from qualified and experienced Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Important properties of z-transforms assignment help -Important properties of z-transforms homework help and Digital signal processing problem's solution with step by step procedure.
Why Expertsmind for Digital signal processing assignment help service
1. higher degree holder and experienced tutors
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. On Time Delivery
5. Privacy of information and details
6. Excellence in solving Digital signal processing queries in excels and word format.
7. Best tutoring assistance 24x7 hours