Important properties of hyperbola:

As the fundamental equation of hyperbola only differs from that of ellipse in having -b² instead of b², it will be found that many propositions for hyperbola are derived from those for the ellipse by changing sign of b². Some of the results for the hyperbola 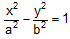 are

(i) The tangent at any point (x₁, y₁) on curve is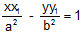 

(ii) The tangent at point 'θ' is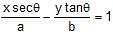 

(iii) The straight line y = mx + c is a tangent to curve, if c² = a² m² - b². Or we can say that y = mx±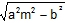touches the curve, for all those values of m when m > b/a or m< -b/a.

(iv) The straight line lx + my = n is a tangent to hyperbola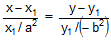  = 1 if n² = a²l² - b²m².

(v) Equation of normal at any point (x₁, y₁) to curve is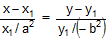 

(vi)   The equation of chord through points θ₁ and θ₂ is

(vii)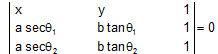  

(viii) The equation of normal at q is ax cosθ + by cotθ = a² + b²

(ix) Through the given point, 4 normals can be drawn to a hyperbola (which are real or imaginary).

(x) Tangent  drawn at any  point  bisects angle   between the lines,  joining the point to foci ,  whereas  normal  bisects  the  supplementary  angle between  lines.

(xi) Equation of director circle is x² + y² = a²- b². This means if a² > b², there would exist many points such that tangents drawn from them would be perpendicular mutually. If
a² < b², no such point exist. For a² = b², centre is only point from which 2 perpendicular tangents (asymptotes) to hyperbola can be drawn.

(xii) A straight line x cos a + y sin a = p is tangent if p² = a² cos² a - b² sin² a.

(xiii) The equation of straight line passing through point (a seca, b tana) and (a secθ', b tanθ') is 

.

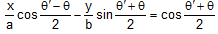Email based Important properties of hyperbola Assignment Help -Important properties of hyperbola Homework Help

We at www.expertsmind.com offer email based Important properties of hyperbola assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.

Expertsmind's best education services

• Quality assignment-homework help assistance 24x7 hrs
• Best qualified tutor's network
• Time on delivery
• Quality assurance before delivery
• 100% originality and fresh work