Implementation For a causal filter whose impulse obtain has even symmetry:

h(n) = h(N-1-n),         for n = 0, 1,..., (N-1) - a total of N points the transfer function 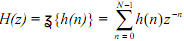may be written, relaying on whether N is odd or even, as follows.

For even N The difference equation is calculate starting from H(z),

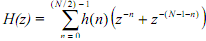
Since Y(z) = H(z) X(z), we can write

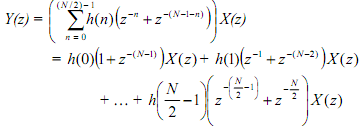
Taking the inverse z-transform of the above we get y(n) as

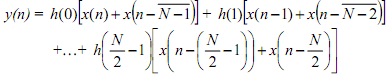
The transferred versions of x(n) are included in pairs and  then multiplied by coefficients h(.). That is given in figure below for N = 8. Note that there are an odd number (= 7) of delay components. There are N/2 = 4 multiplications and (N/2) + 1 = 4 + 1 = 5 adders.

Figure for N = 8

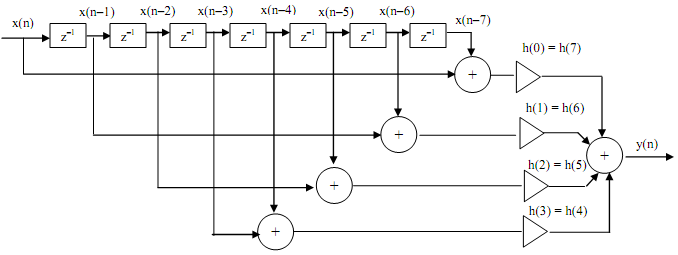
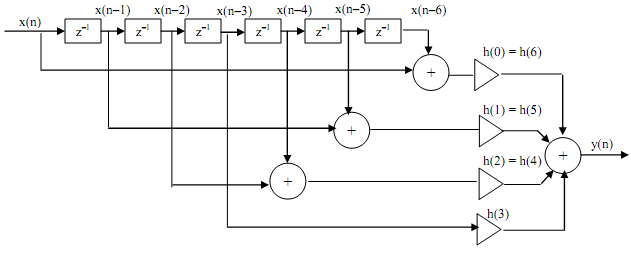
For odd N We need not derive the equations (they would be necessary if we were writing a computer program to automate it). For N = 7, there are N - 1 = 6 delay elements - an even number of delay elements. There are (N + 1)/2 = (7 + 1)/2 = 4 multiplications and 4 adders (the number of two-operand additions is 6).

Figure for N = 7

Email based Implementation For a causal filter assignment help - Implementation For a causal filter homework help at Expertsmind

Are you finding answers for Implementation For a causal filter based questions? Ask Implementation For a causal filter questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Implementation For a causal filter assignment help -Implementation For a causal filter homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours