IIR Digital Filters:
Nomenclature With a0 = 1 in the linear constant coefficient difference equation,
a0 y(n) + a1 y(n-1) + ... + aN y(n-N) = b0 x(n) + b1 x(n-1) + ... + bM x(n-M), a0≠ 0
we have,
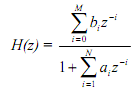
This represents an IIR filter if at least one of a1 through aN is nonzero, and all the roots of the denominator are not canceled exactly by the roots of the numerator. In general, there are M finite zeros and N finite poles. There is no restriction that M should be less than or greater than or equal to N. In most cases, especially digital filters derived from analog designs, M ≤ N. Systems of this type are called Nth order systems. This is the case with IIR filter design in this Unit.
When M > N, the order of the system is no longer unambiguous. In this case, H(z) may be taken to be an Nth order system in cascade with an FIR filter of order (M - N).
When N = 0, as in the case of an FIR filter, according to our convention the order is 0. However, it is more meaningful in such a case to focus on M and call the filter an FIR filter of M stages or (M+1) coefficients.
Example The system H(z) = (1 - z -8 ) (1 - z -1 ) is not an IIR filter. Why (verify)?
IIR filter design An analog filter specified by the Laplace transfer function, Ha(s), may be designed to either frequency domain or time domain specifications. Similarly, a digital filter, H(z), may be required to have either (1) a given frequency response, or (2) a specific time domain response to an impulse, step, or ramp, etc.
Analog design using digital filters, ωi = ΩiT Another possibility is that a digital filter may be required to simulate a continuous-time (analog) system. To simulate an analog filter the discrete- time filter is used in the A/D - H(z) - D/A structure shown below. The A/D converter can be thought of roughly as a sampler and coder, while the D/A converter, in many cases, represents a decoder and holder followed by a low pass filter (smoothing filter). The A/D converter may be preceded by a low pass filter, also called an anti-aliasing filter or pre-filter.
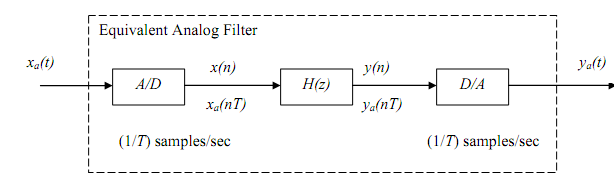
We will usually be given a set of analog requirements with critical frequencies Ω1, Ω2,..., ΩN in radians/sec., and the corresponding frequency response magnitudes K1, K2, ..., KN in dB. The sampling rate 1/T of the A/D converter will be specified or can be determined from the input signals under consideration.
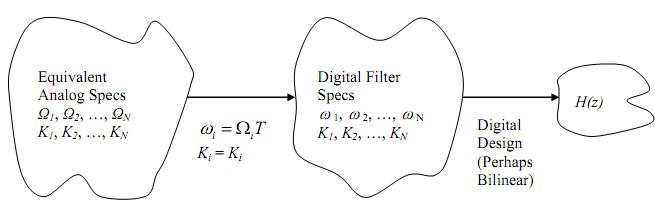
The general approach for the design is to first convert the analog requirements to digital requirements and then design the digital filter using the bilinear transformation. The conversion of the analog specifications to digital specifications is through the formula ωi = ΩiT. To show
that this is true, suppose that the input to the equivalent analog filter is xa(t) = sin Wit . The output
of the A/D converter with sampling rate 1/T becomes
x(n) = xa(nT) = sin Ωi nT = sin (ΩiT )n = sin Ωi n
Thus, the magnitude of the discrete-time sinusoidal signal is the same as the continuous time sinusoid, while the digital frequency ωi is given in terms of the analog frequency Ωi by ωi = ΩiT.
Thus, the specifications for the digital filter become ω1, ω2, ..., ωN with the corresponding frequency response magnitudes K1, K2, ..., KN. The digital frequency, ω, is in units of radians. The procedure is conceptually shown in figure below.
There are various techniques for designing H(z):
1. Numerical approximation (numerical solution) to the derivative operation or the integration operation (this latter results in the bilinear transformation aka bilinear z-transformation - BZT).
2. Time domain invariance, e.g., impulse invariance and step-invariance methods.
The focus is on the low pass analog filter because once designed it can be transformed into an equivalent quality high pass, band pass or band stop filter by frequency transformation. The Butterworth, Chebyshev and elliptic filters are used as a starting point in designing digital filters. We approximate the magnitude part of the frequency response, not the phase. Butterworth and Chebyshev filters are actually special cases of the more difficult elliptic filter.
Because a constant divided by an Nth order polynomial in Ω falls off as ΩN it will be an approximate low pass function as Ω varies from 0 to ∞. Therefore, an all-pole analog filter H(s) = 1/D(s) is a good and simple choice for a low pass filter form and is used in both the Butterworth and the type I Chebyshev filters. Moreover, for a given denominator order, having the numerator constant (order zero) gives (for a given number of filter coefficients) the maximum attenuation as Ω → ∞.
Email based IIR Digital Filters assignment help - IIR Digital Filters homework help at Expertsmind
Are you finding answers for IIR Digital Filters based questions? Ask IIR Digital Filters questions and get answers from qualified and experienced Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer IIR Digital Filters assignment help -IIR Digital Filters homework help and Digital signal processing problem's solution with step by step procedure.
Why Expertsmind for Digital signal processing assignment help service
1. higher degree holder and experienced tutors
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. On Time Delivery
5. Privacy of information and details
6. Excellence in solving Digital signal processing queries in excels and word format.
7. Best tutoring assistance 24x7 hours