Height Balanced Trees

The effectiveness of the searching process in a binary search tree depends on how data are organized to make up a specific tree. 

            A binary tree of height h is completely balanced if all leaves occur at nodes of level h or h-1 and if all nodes at levels lower than h-1 have two children. According to this definition the tree in Figigure is balanced because all leaves occur at level 3 considering at level 1 and all node s at levels 1and2 have two children. Intuitively we might consider a tree to be well balanced if for each node the longest paths from the left of the node are about the same length as the longest paths on the right.

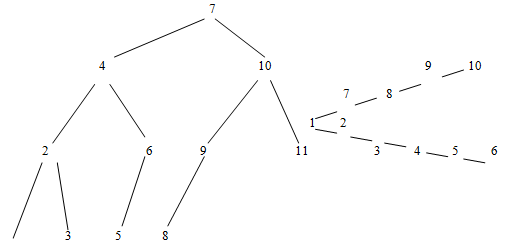
More precisely, a tree is height balanced if, for each node in the tree, the height of the left sub tree differs from the height of the right sub tree by no more than 1. The tree in Fig height balanced but it is not completely balanced. On the hand the tree in Figiure  is completely balanced tree.

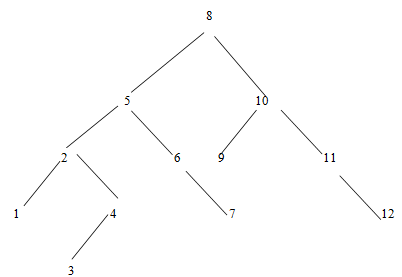
An almost height balanced tree is called an AVL tree after the Russian mathematician G.M. Adelson-Vleskii and E.M. Lendis, who first defirted and studied this form of a tree. AVL Tree may or may not be perfectly balanced.

Let us determine how many nodes might be there in a balanced tree of height h.

The root will be the only node at level 1;

Each subsequent level will be as full as possible i.e. 2 nodes at level 2,4 nodes at level 3 and so on i. e. in general there will be 2^{1 -1} nodes at level 1. Therefore the number of nodes from level 1 through level h-1 will be

                       1+2+2²+2³ +...............+ 2^{h-2 =}2^h-1- 1

The number of nodes at level h may range from a single node to a maximum of 2 h-1 node. Therefore the total number of nodes of nodes n of the tree may range of (2h-1-1+1) or 2h-1 to 2h-1.

Building Height Balanced Tree

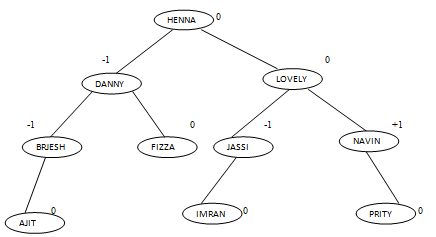
Each node of an AVL tree has the property that the height of the left sub tree is either on more, equal or one less than the height of the right sub tree. We may define a balance factor (BF) as BF = (Height of Left sub tree-Height of Right sub tree)

               Further

               If two sub tree are of same height BF =0

               If right sub tree is higher BF =+1

               If left sub tree is higher       BF =-1

For example balance factor are stated near the nodes is Figure of the root node is zero because height of the right sub tree and the left sub tree is three. The BF at the node DINsi-17 because the height of its left sub tree is 2 and of right sub tree is 1 etc.

Data Structure & Algorithms Assignment Help, Live Experts 

Struggling with data structure problems? Data structure subject is quite tough to learn? Need quick assistance in data structure questions? ExpertsMind.com is right place for you where your search ends, We at ExpertsMind offer online data structure assignment help, data structure homework help and data structure and algorithms question's answers by best online support by qualified tutors.

ExpertsMind.com - Height Balanced Trees Assignment Help, Height Balanced Trees Homework Help, Height Balanced Trees Assignment Tutors, Height Balanced Trees Solutions, Height Balanced Trees Answers, Binary Trees Assignment Tutors