Greibach Normal Form:

Every CFG G can also be converted to an equivalent grammar in Greibach Normal Form. A context-free grammar G = (V, Σ, P, S) is in Greibach Normal Form iff its productions are of the form shown below

A → aBC,

A → aB,

A → a,      or

S → ∈,

where A, B, C ∈ N ,a ∈ Σ, S → ∈ is in P iff ∈ L(G), and S  does not occur on the right-hand side of the production.

Note that a grammar in Greibach Normal Form does not contain rules other than possibly S →∈. More importantly,  except the special rule S → ∈, every rule produces some terminal symbol.

A significant consequence of the Greibach Normal Form is that every nonterminal is not left recursive.  A nonterminal A  is left recursive iff A 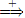 Aα  for α ∈ V*.  Left recursive nonterminals cause top-down determinitic  parsers to loop. The Greibach Normal Form provides a method of avoiding this problem.

There are no easy proofs that every CFG is converted to a Greibach Normal Form. A particularly elegant method because of Rosenkrantz by using least fixed-points.

Lemma 3.6.1   Given a context-free grammar G = (V, Σ, P, S), 1 can construct a context- free grammar G' = (V', Σ,P', S') such that L(G') = L(G) and G'  is in Greibach Normal Form, which means that, a grammar whose productions are of the form the

A → aBC,

A → aB,

A → a,      or

S' → ∈,

here A, B, C  ∈ N', a ∈ Σ, S' →∈ is in P' iff ∈ L(G), and S'  does not occur on right-hand side of any production in P'.

Email based Automata assignment help - homework help

The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help - Automata homework help and online tutoring with best qualified and experienced computer science tutor's help. We cover all topics including Greibach Normal Form in assignment help - homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.