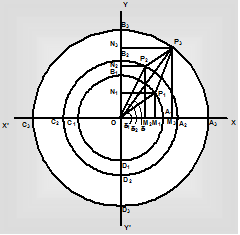
Graphical method of finding the resultant of two S.H.M.'s in the same direction when they have the same periodic time: Suppose that a particle N possesses simultaneously two simple harmonic motions about O in the direction YOY′ or the Y axis and the periodic time of each equals T. Let the amplitudes of the two simple harmonic motions be a₁ and a₂ and their epoch angles  and  respectively. With O as centre and radii = a₁ and a₂, draw circles A₁B₁C₁D₁ and A₂B₂C₂D₂ cutting the axes of X and Y at the points shown in figure. Take the points P­₁ and P₂ on the circumferences of the two circles such that ∠P₁OX = δ₁ and ∠P2OX = δ₂. From P₁ and P₂ draw P₁N₁ and P₂N₂ perpendiculars on YOY′ and P₁M₁

and P₂M₂ perpendiculars on XOX′. Then ON₁ and ON₂ denote the component displacements y₁ and y₂ of the particle N at the start. With OP₁ and OP₂ as sides, complete the parallelogram OP₁P₃P₂ and join OP₃. Draw P₃N₃ and P₃M₃ perpendiculars on YOY′ and XOX′ respectively. The resultant displacement of the particle N on Y-axis at the start is given by ON₃. Let this be denoted by y.

Since    N₂N₃ = ON₁ = y₁

            y = ON₃ = ON₂+N₂N₃ = y₂+y₁

With O as centre and radius = OP₃, draw the circle A₃B₃C₃D₃. Since the components having simple harmonic vibrations have the same periodic time T, the angular velocities OP₁ and OP₂

will be same  and the resultant OP₃ will also rotate with the same angular velocity as OP₁ or OP₂. Thus P₃ will always lie on the circumference A₃B₃C₃D₃. The resultant motion of the particle N being the projection of uniform circular motion of P₃ will therefore, be simple harmonic motion about O along YOY′ with periodic time T. The amplitude of the resultant is given by the diagonal of the parallelogram.

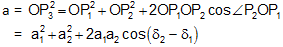
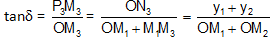
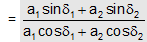
The epoch angle of the resultant = d = P3OX is given by                           We, therefore, find that the resultant of two simple harmonic motions of equal period in the same direction is another simple harmonic motion of the same period, but of amplitude given by compounding the component amplitudes according to the Parallelogram law.

Special Cases

(i) When δ₁ = δ2 = f, i.e. the two simple harmonic vibrations are in the same phase δ2 - δ1 = 0 and

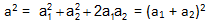
or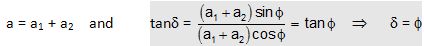         

The resultant vibration has, therefore, in this case, amplitude equal to the sum of the amplitudes of component vibrations and is in phase with each of them.

(ii) When δ₂ - δ₁ = 180°or component vibrations are opposite in phase then

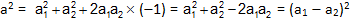
or         a  = a₁ - a₂

and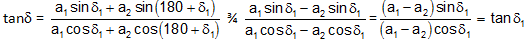      

or       

The resultant vibration has thus amplitude equal to the difference of amplitudes of component vibrations and is in phase with one of the component vibrations - the one with the bigger amplitude.

Email based Physics assignment help - homework help at Expertsmind

Are you searching physics expert for help with Graphical method of simple harmonic motion questions?  Graphical method of simple harmonic motion topic is not easier to learn without external help?  We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Graphical method of simple harmonic motion related problems. We provide step by step Graphical method of simple harmonic motion question's answers with 100% plagiarism free content. We prepare quality content and notes for Graphical method of simple harmonic motion topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.

Why Expertsmind for assignment help

1. Higher degree holder and experienced experts network
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. Time on Delivery
5. Privacy of information and details
6. Excellence in solving physics queries in excels and word format.
7. Best tutoring assistance 24x7 hours