General procedure for the partial fraction expansion
Since X(z)/z should be rational, it takes the form
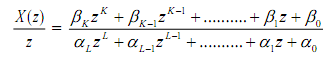
If K < L then no adjustment is required. The partial fraction expansion is straightforward.
If K ≥ L then divide until the remainder polynomial in z has the degree of L-1 or less:
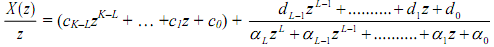
The 1st part of the above expression, (cK-LzK-L + ... +c1z + c0), will eventually contribute δ functions to output sequence some of themare time-advanced such that the resulting x(n) will be noncausal. The 2nd part - the proper fraction - is expanded into the partial fractions. Suppose that we have 1 repeated pole of order m, call it z1, and all the rest are distinct, call them zm+1, zm+2,..., zL. Then let
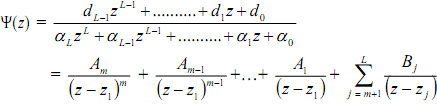
The coefficients Aj (m of them) and Bj (L - m of them) are found as follows:
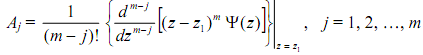
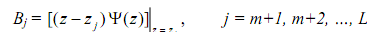
In resulting x(n) the contribution of Aj terms is several exponentials multiplied by n, (n-1), (n-2), etc., and the contribution of the Bj terms is several complex exponentials.
Email based General procedure for the partial fraction expansion assignment help - General procedure for the partial fraction expansion homework help at Expertsmind
Are you finding answers for General procedure for the partial fraction expansion based questions? Ask General procedure for the partial fraction expansion questions and get answers from qualified and experienced Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer General procedure for the partial fraction expansion assignment help -General procedure for the partial fraction expansion homework help and Digital signal processing problem's solution with step by step procedure.
Why Expertsmind for Digital signal processing assignment help service
1. higher degree holder and experienced tutors
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. On Time Delivery
5. Privacy of information and details
6. Excellence in solving Digital signal processing queries in excels and word format.
7. Best tutoring assistance 24x7 hours