Frequency response of discrete-time system
For the linear shift-invariant system with impulse response h(n), the Fourier transform H(ω) gives the frequency response. Consider input sequence x(n) = e jwn for -∞ < n < ∞, i.e., a complex exponential of radian frequency ω and magnitude 1, applied to the linear shift-invariant system whose unit sample response is h(n). By using convolution we obtain the output y(n) as
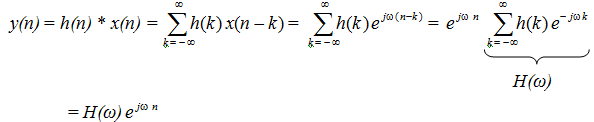
Therefore we see that H(ω) describes change in the complex amplitude of a complex exponential as a function of frequency. The quantity H(ω) is called as frequency response of the system.
Generally, H(ω) is complex valued and can be expressed either in the Cartesian form or the polar from as
H(ω) = HR(ω) + jHI (ω) or H(ω) = Hˆ (w) e j∠H(w)
here HR and HI are respectively the real part and imaginary part. Hˆ (w) is called as magnitude and H (w ) is called as phase. Strictly speaking, Hˆ (w) is called as zero- phase frequency response; note that Hˆ (w) is real valued but can be positive or negative. We can use the symbol |H(ω)| for magnitude which is non-negative. If Hˆ (w) is positive then
Magnitude = H (w) = Hˆ (w) & Phase = ∠H (w )
If Hˆ (w) is negative then
Magnitude = H (w) = Hˆ (w) = -Hˆ (w) & Phase = ∠H (w ) ± π
We shall often freely use the symbol H (w) 
to refer to Hˆ (w) as well with the understanding that when latter is negative we shall take its absolute value and accordingly adjust ∠H (w ) by ± π.
Example The impulse response of LTI system
y(n) = x(n) + x(n -1) + x(n - 2)/3
is
h(n) = 1/3, n = 0, 1, 2
0, otherwise
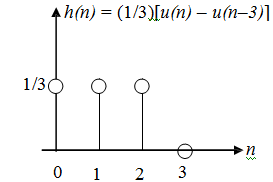
The frequency response can be obtained as follows.
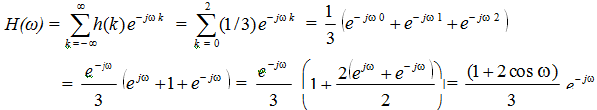
which is already in the polar form H (w) = ± H (w) e∠jH (w ) , such that
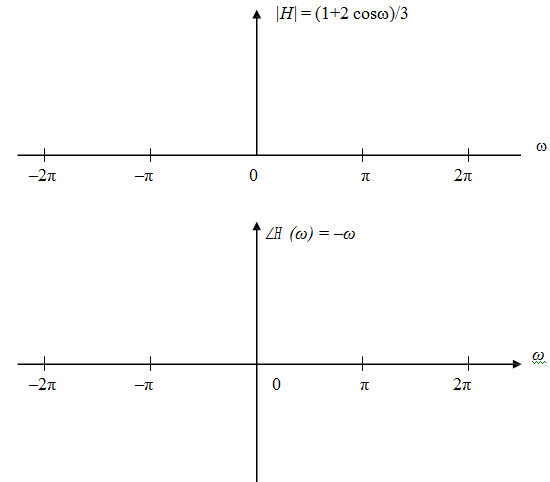
H (w) = (1 + 2 cos w) / 3 and ∠H (w) = -ω
The zero crossings of magnitude plot occur where H (w) = (1 + 2 cos w) / 3 = 0, or ω = cos -1 (-1 / 2) = 2π/3 = 1200. A frequency of ω = 2π/3 rad./sample (f = 1/3 cycle/sample) is stopped completely by the filter. The corresponding digital signal is x5(n) = cos 2π(1/3)n. The continuous-time signal, x5(t), depends on sampling frequency. If, for instance, the sampling frequency is 16Hz, then x5(t) = cos 2π(16/3)t, and a frequency of 16/3 Hz will be filtered out completely. If the sampling frequency is 150Hz, then x5(t) = cos 2π(150/3)t, and a frequency of 50 Hz will be removed.
In calibrating horizontal axis in the terms of the cyclic frequency, F, we use relation ω = ΩT = 2πFT = 2πF/Fs from which the point ω = 2π corresponds to F = Fs.
(Aside) The system y(n) = x(n)/3 + x(n - 1)/3 + x(n - 2)/3 is a crude low pass filter, but the attenuation does not increase monotonically with frequency. In fact, the highest possible frequency, Fs/2 Hz, (or π rad/sample) is not well attenuated at all. The following is a slight variation of the three-term moving average:
y(n) = x(n)/4 + x(n - 1)/2 + x(n - 2)/4
Its magnitude response is a "raised cosine" (with no zero crossing, monotonically decreasing but wider than the 3-term).
Email based Frequency response of discrete-time system assignment help - Frequency response of discrete-time system homework help at Expertsmind
Are you finding answers for Frequency response of discrete-time system based questions? Ask Frequency response of discrete-time system questions and get answers from qualified and experienced Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Frequency response of discrete-time system assignment help -Frequency response of discrete-time system homework help and Digital signal processing problem's solution with step by step procedure.
Why Expertsmind for Digital signal processing assignment help service
1. higher degree holder and experienced tutors
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. On Time Delivery
5. Privacy of information and details
6. Excellence in solving Digital signal processing queries in excels and word format.
7. Best tutoring assistance 24x7 hours