Fast Fourier transform:

For a finite-duration sequence x(n) of length N, the DFT sum may be written as

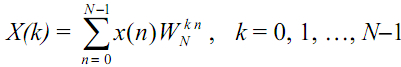
where W_N = e ^{- j 2p / N .}There are the total of N values of X(.) ranging from X(0) to X(N-1). The calculation of X(0) includes no multiplications at all as every product term involves W₀   = e^{- j 0}  = 1. Further, the first term in the sum always includes W₀ or e^{- j 0}  = 1 and thus does not need a multiplication. Each X(.) calculation other than X(0) thus involves (N-1) complex multiplications. And each X(.) involves (N-1) complex additions. Since there are N values of X(.) the overall DFT requires ( N - 1)2 complex multiplications and N(N-1) complex additions. For

large N we may round these off to N₂ complex multiplications and the same number of complex additions. 

Each complex multiplication is of the form

(A + jB) (C + jD) = (AC - BD) + j(BC + AD)

and thus requires 4 real multiplications and 2 real additions. Each complex addition is of the form

(A + jB) + (C + jD) = (A + C) + j(B + D)

and needs 2 real additions. Therefore the computation of all the N values of DFT requires 4N² real multiplications and 4N² (= 2N² + 2N² ) real additions.

The efficient algorithms which reduce number of multiply-and-add operations are known by name of the fast Fourier transform (FFT). The Cooley-Tukey and Sande-Tukey FFT

algorithms exploit following properties of twiddle factor, W_N = e^{- j 2p / N}

(the factor e^{j 2p/N} is called the Nth principal root of 1):

1.   Symmetry property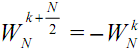 

2.   Periodicity property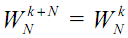 

To show, the case of N = 8, these properties result in following relations:

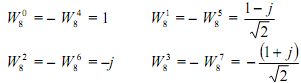
The use of these properties decreases the number of complex multiplications from N² to N  (in fact the number of multiplications is less than this as a number of the multiplications by W_r are really multiplications by ±1 or ±j and do not count); and the number of complex additions are reduced from N² to N log N. Therefore, with each complex multiplication requiring 4 real multiplications and 2 real additions and each complex addition requiring 2 real additions, the computation of all N values of the DFT requires

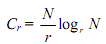
We can get a rough comparison of the speed advantage of an FFT over a DFT by computing the number of multiplications for each since these is usually more time consuming than the additions. For instance, for N = 8 the DFT, using the above formula, would need 8² = 64 complex multiplications, but the radix-2 FFT requires 12 (= 8/2 log₂ 8 = 4 x 3).

Number of multiplications: DFT vs. FFT

We consider 1st the case where the length N of sequence is an integral power of 2, that is, N = 2^ν here ν is an integer. These are known as radix-2 algorithms of which the decimation-in-time (DIT) version is also called as the Cooley-Tukey algorithm and the decimation-in-frequency (DIF) version is called as the Sande-Tukey algorithm. We show 1st how the algorithms work; their derivation is given later.

For a radix of (r = 2), the elementary computation (EC) called as the butterfly consists of a single complex multiplication and 2 complex additions.

If the number of points, N, can be expressed as N = r^m , and if computation algorithm is carried out via a succession of r-point transforms, the resultant FFT is known as radix- r algorithm. In the radix-r FFT, an elementary computation comprises of an r-point DFT followed by multiplication of r results by suitable twiddle factor. The number of ECs required is

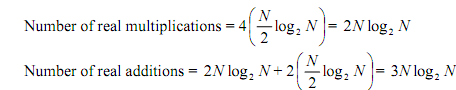
which decreases as r increases. Certainly, the complexity of an EC increases with the increasing r. For r = 4, the EC requires 3 complex multiplications and several complex additions.

Assume that we desire an N-point DFT where N is a composite number which can be factored into product of integers

N = N₁ N₂ ... N_m

If, for example, N = 64 and m = 3, we might factor N into product 64 = 4 x 4 x 4, and the 64- point transform can be seen in a 3-dimensional 4 x 4 x 4 transform.

If N is the prime number so that factorization of N is not possible, the original signal can be zero-padded and the resulting new composite number of the points can be factored.

Email based Fast Fourier transform assignment help - Fast Fourier transform homework help at Expertsmind

Are you finding answers for Fast Fourier transform based questions? Ask Fast Fourier transform questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Fast Fourier transform assignment help -Fast Fourier transform homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours