Family of lines:
Assume that L1= a1x+b1y+c1 = 0 and L2=a2x + b2y + c2 = 0 are the two intersecting lines and let the point of their intersection be (α, β). Now if we write these 2 equations in this form L1 + λL2 (where λ is a parameter)
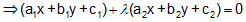.........(1)
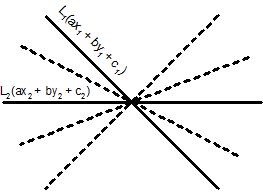
then for the different values of λ, (1) will give different straight lines.
Now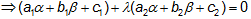 
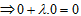
=>(α, β) always lies on (1) does not matter what is the value of λ.
Therefor (1) represent a family of straight lines passing through the point of intersection of a1x+b1y+c1 = 0 and a2x + b2y + c2 = 0.
Note:
- When we have to show that the line always passes through a fixed point, we use the concept of family of lines.
- Family of lines perpendicular to the given line ax+by+c = 0 is given by bx-ay+k=0, here k is a parameter.
- Family of lines parallel to the given line ax+by+c = 0 can be given by ax+by+k=0, where k is a parameter.
Illustration: Find the equation of straight line which belongs to both the family of lines 5x + 3y - 2 + l1 (3x - y - 4) = 0 and x - y + 1 + l2 (2x - y - 2) = 0
Solution. Lines of 1st family are concurrent at (1, -1) and that of 2nd at (3, 4)
∴ The required line passes through both these points
∴ Equation is 5x - 2y - 7 = 0
Email based Family of lines Assignment Help -Family of lines Homework Help
We at www.expertsmind.com offer email based Family of lines assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.
Expertsmind's best education services
- Quality assignment-homework help assistance 24x7 hrs
- Best qualified tutor's network
- Time on delivery
- Quality assurance before delivery
- 100% originality and fresh work