Example of closure
Constructing the equivalent DFA
Let Mn = (Q, Σ, δ, s, F) be any NFA. We construct the DFA Md =(2Q, Σ, δ', E(s), F'), here :
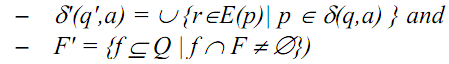
|
E(q0)
|
E(q1)
|
E(q2)
|
E(q3)
|
E(q4)
|
|
q0, q1, q2, q3
|
q1, q2, q3
|
q2
|
q3
|
q3,q4
|
Prove property of δ and δ'
Let Mn = (Q, Σ, δ, s, F) be any NFA, and Md = (2Q, Σ, δ', E(s), F') be a DFA, where
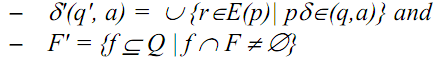
Prove 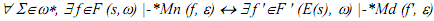 by induction.
by induction.
Prove a general statement 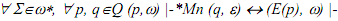
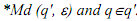
Proof
Part I:
For any string w in Σ*, and states q and r in Q, there is R ⊆ Q so that
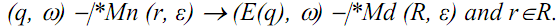
Basis:
Let ω be a string in Σ*, q and r be states in Q, and (q, w) -|*Mn (r, ε) in 0 step. Because (q, w) -|*Mn (r, ε) in 0 step, we know (1) q=r , and (2) w= ε.
Then, (E(q), w) = (E(r), ε).
Thus, (E(q), w) -|*Md (E(r), ε) .
That is, there exists R=E(r) such that r ∈ R and (E(q),w) -|*Md (R, ε). Induction hypothesis:
For any non-negative integer k, string w in Σ*, and states q and r in Q, there is R⊆Q:
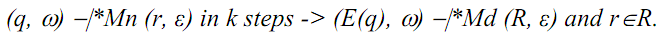
Induction step:
Prove, for any non-negative integer k, string w in Σ*, and states q and r in Q, there exists R ⊆ Q:
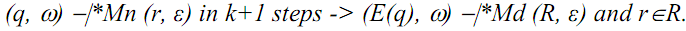
Let w be a string in Σ*, q and r be states in Q, and (q, w) -|*Mn (r, ε) in k+1 steps.
Because (q, w) -|*Mn (r, ε) in k+1 steps and k≥0, there exists a state p in Q and a string ∈aΣ* so that (q, w) -|*Mn (p, a) in k steps and (p, a) -|Mn (r, ε) for some a∈Σ∪{ε}.
From the induction hypothesis and (q, w) -|*Mn (p, a) in k steps, we know that there exists P⊆Q so that (E(q), w) -|*Md (P, a) and p∈P. Since (p, a) -|Mn (r, ε), rδ∈(p, a).
From definition of δ' of Md, E(δ(p, a))⊆δ'(P, a) as p∈P.
Because rδ∈(p, a) and E(d(p, a))⊆δ'(P, a), r'δ∈(P, a).
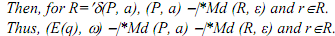
Part II:
For any string w in Σ*, and states q and r in Q, there exists R ⊆ Q such that r∈R and
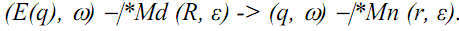
Proof
Basis:
Let w be a string in Σ*, q and r be states in Q, R be a subset of Q such that r ∈ R and
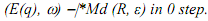
Because (E(q),w) -|*Md (R, ε) in 0 step, E(q)=R and ω=ε.
From the definition of E, δ'(q, ε)=R because E(q)=R. Then, for any r∈R, (q, ω) -|*Mn (r, ε).
That is, there exists R=E(q) such that r ∈ R and (q, ω) -|*Mn (r, ε). Induction hypothesis:
For any non-negative integer k, string w in Σ*, and states q and r in Q, there exists R⊆Q such that r∈R and:
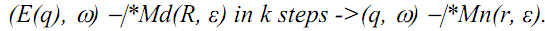
Prove, for any non-negative integer k, string w in Σ*, and states q and r in Q, there exists R ⊆ Q such that r∈R:
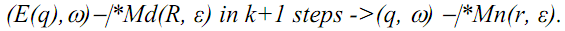
Let w be a string in Σ*, q and r be states in Q, and (E(q), w) -|*Md (R, ε) in k+1 steps.
Because (E(q), w) -|*Md (R, ε) in k+1 steps and k≥0, there exists P∈2Q (i.e. P⊆Q) and a string ∈aΣ* such that ω=aa, (E(q), a) -|*Md (P,ε) in k steps and (P, a) -|Md (R, ε) for some a∈Σ.
From the induction hypothesis and (E(q), a) -|*Md (P, ε) in k steps, we know that there exists p∈P such that (q, a)-|*Mn(p,ε) (i.e. (q, aa) -|*Mn (p, a) ).
Since (P, a) -|Md (R, ε), there exists r∈R such that r= δ(p, a).
Then, for some r∈R, (p, a) -|*Mn (r, ε).
Thus, (q, w) -|*Mn (p, a) -|*Mn (r, ε) for some r∈R.
Email based Automata assignment help – homework help
The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help – Automata homework help and online tutoring with best qualified and experienced computer science tutor’s help. We cover all topics including Example of closure in assignment help – homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.