Example of Chomsky Normal Form:

Given a context-free grammar G = (V, Σ, P, S), 1 can construct a context- free grammar G' = (V', Σ,P', S') such that:

(1) L(G')= L(G);

(2) P' contains no-rules other than S' →  , and S' →   ∈ P'   iff   ∈ L(G);

(3) S'  does not take place on right-hand side of production in P'.

Proof . We begin by proving that E(G)= Ei0 . For specifically this, we prove that E(G) ⊆ E_i0  and E_i0  ⊆ E(G).

To prove that E_i0  ⊆ E(G), we continue by induction on i.  As E₀ = {A ∈ N  | (A →∈) ∈ P }, we have  A⇒∈, and hence A  ∈ E(G).   By the induction  hypothesis, Ei ⊆ E(G). If A ∈ E_i+1 , either A ∈ Ei  and then A ∈ E(G), or there is production (A  → B1  ... Bj ... Bk ) ∈ P , such that Bj  ∈ Ei  for all j, 1 ≤ j ≤ k.  By induction hypothesis, B =>∈ for each j,1 ≤ j ≤ k, and therefore

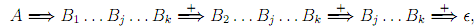
which signifies that A ∈ E(G).

To prove that E(G) ⊆ E_i0 , we also proceed by induction,  but on the length of a derivation A . If A =>∈, then A →∈ P , and thus A ∈ E₀ as E₀ = {A ∈ N  | (A →∈) ∈ P }.

If A =>∈, then

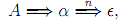
for some production  A → α ∈ P . If α contains terminals of nonterminals not in E(G), it is not possible to derive   from α, and thus, we should have α = B1  ... Bj ... Bk , with Bj ∈ E(G), for all j, 1 ≤ j ≤ k.  But, Bj => ∈ where nj  ≤ n, and by the induction hypothesis,B_j ∈ E_i0 . But then, we get A ∈ E_i0 +1 = E_i0, as desired.

Having shown that E(G)= Ei0 , we construct  grammar G'. First, we create the production  S'→ S  where S' ∈/  V , to make sure that S'  does not occur on right-hand side of any rule in P'. Let

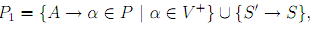
and let P2  be the set of productions

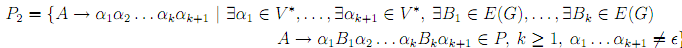
Keep in mind that ∈ L(G) i? S ∈ E(G). If S ∈/ E(G), then let P'= P1 ∪ P2, and if S ∈ E(G), then let P'= P1 ∪ P2 ∪ {S' →∈ }. We claim that L(G')= L(G), which can proved by showing that every derivation using G can be simulated by a derivation using G', and vice-versa. All conditions of the lemma are now achived.

From a practical point of view, the construction  or lemma is quite costly. for instance, given a grammar containing the productions

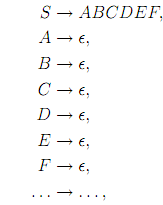
eliminating the   rules will create 2⁶  - 1 = 63 new rules corresponding  to 63 nonempty subsets of set {A, B, C, D, E, F }. Now turn to elimination of chain rules.

It turns out that matters are simplified greatly if we 1st apply lemma 3.3.1 to the input grammar G, and we explain the construction assuming that G = (V, Σ, P, S) satisfies the conditions of lemma. For every nonterminal A ∈ N , we describe the set

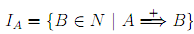
The sets IA are computed by using approximations I_A,i can be defined as follows:

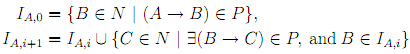
Obviously, for every A ∈ N , the I_A,i form the ascending chain

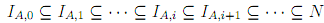
and as N  is finite, there is a least i, say i0, such that 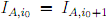We claim that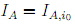 

Email based Automata assignment help – homework help

The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help – Automata homework help and online tutoring with best qualified and experienced computer science tutor’s help. We cover all topics including Example of Chomsky Normal Form in assignment help – homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.