Equivalence of NTM and DTM:

Theorem:

For any NTM Mn, there is a DTM Md such that:

-   if Mn halts on input a having output b, then Md halts on input a with output b, and

-   if Mn does not stop on input a, then Md does not stop on input a.

Proof:

Let Mn =  (Q, Σ, Γ, δ, s) be an NTM.

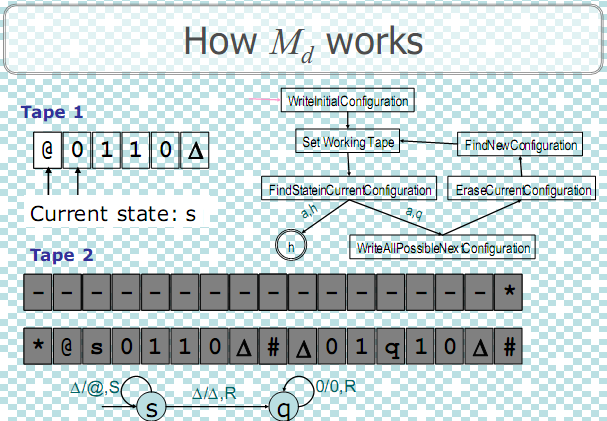
• Then, there exists a positive integer n so that the initial configuration (s, Δα) of Mn yeilds a halting configuration (h, Δβ) in n steps.

• From construction of Md, the configuration (h, Δ β ) should appear on tape 2 at some time.
• Then, Md should halt with b on tape 1.

if Mn does not halt on input a

• Then, Mn cannot reach halting configuration. Which means that, (s, Δα) never yields a halting configuration (h,  Δβ).

•   From the construction of Md, configuration (h,Δβ) never appears on tape 2.

• Then, Md never stop.

Email based Automata assignment help - homework help

The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help - Automata homework help and online tutoring with best qualified and experienced computer science tutor's help. We cover all topics including Equivalence of NTM and DTM in assignment help - homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.