In general the total energy of a harmonic oscillator consists of two parts, potential energy (P.E) and kinetic energy (K.E.), the former being due to its displacement from the mean position and latter due to its velocity. Since the position and velocity of the harmonic oscillator are continuously changing, P.E. and K.E. also change but their sum i.e., the total energy (T.E) must have the same value at all times.
(i) Potential Energy: The simple restoring force acting on the harmonic oscillator is given by
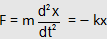
Now if the oscillator is displaced through a further displacement dx opposite the force, work done in displacing the object is given by
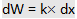
Hence the net work done in displacing the object from mean position (x=0) to (x=x) is given by
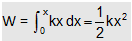
By convention, P.E. at the mean position is given as zero. Hence, above relation gives the magnitude of P.E. of harmonic oscillator at a distance x from the mean position i.e.,
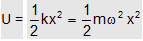 . . . (i)
. . . (i)
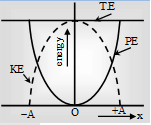
This shows the P.E. is proportional to the square of the displacement and graph showing the variation of potential energy with the displacement will be a parabola given by continuous lines in the figure. P.E. is maximum at maximum distance and is given by
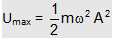
(ii) Kinetic Energy: Speed of harmonic oscillator is given by equation as
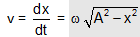
Hence kinetic power of the oscillator is provided by
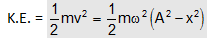 . . . (ii)
. . . (ii)
|
The graph showing the variation of K.E. with x is shown in figure by dotted lines.
The kinetic energy is biggest when x = 0. Thus
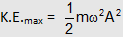
Now net energy E of the oscillator for distance x is given by
|
|
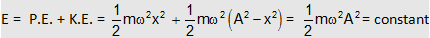 (iii)
(iii)
Thus total energy is independent of the distance. It has constant throughout the motion of the oscillator. Also the net energy is same to maximum value of either K.E. or P.E.
(iii) Average Value of P.E. and K.E.: By equation (i) P.E. at distance x is given by
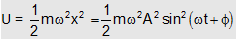
The average value of P.E. for one complete oscillation is given by
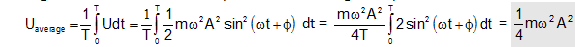
Because the average magnitude of sine or of cosine function for the complete cycle is equal to zero.
Now K.E. at x is given by
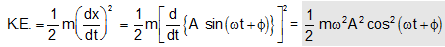
The average value of K.E. for one complete cycle
KEaverage = 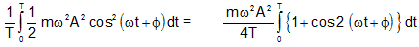
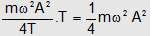
Thus average values of P.E. and K.E. of harmonic oscillator are equal and each is equal to one fourth of the total energy.
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Energy of a body in Simple harmonic motion questions? Energy of a body in Simple harmonic motion topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Energy of a body in Simple harmonic motion related problems. We provide step by step Energy of a body in Simple harmonic motion question's answers with 100% plagiarism free content. We prepare quality content and notes for Energy of a body in Simple harmonic motion topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours