FORCE ON THE PARTICLE: For a mass m to have acceleration, a force provided by F = ma is always needed. In uniform circular motion, acceleration is of value v2/t and is directed tends to centre. Hence a force of magnitude mv2/r is needed to keep a particle in circular motion. This force is called as the centripetal force. After studying the given examples, you should carefully notice that the centripetal force is not an extra force on an object. Whatever force is responsible for circular motion converts into the centripetal force.
When a satellite moves around the earth, the gravitational attraction of earth behaves like as the centripetal force for the circular motion of the satellite; when an electron moves around the nucleus in an atom. The electrostatic attraction of nucleus behaves like as the centripetal force for the electron's circular motion. In case of a conical pendulum, T sin q converts into the centripetal force.
Main steps for analyzing forces in uniform circular motion: Consider one axis along the radius of circle (i.e. in direction of acceleration) and other axis perpendicular to the radius. Resolve all the forces into horizontal and vertical components.
Net force along perpendicular axis = zero
Total force along radial axis (towards centre) = mv2/r=mw2r
Main phase for analyzing forces in Non-Uniform Circular Motion: After resolving all the forces along radial and tangential axes:
Net tangential force = Ft = m at
Net radial force = Fr = m ar = mv2/r
The most common example of non-uniform circular motion is the motion of particle in vertical circle. If a particle is moved in a vertical circle with the help of a string,
The forces are called tension (T) towards centre and weight (mg).
In type of a particle moving along the outside surface of a circular track, the forces are: Normal reaction (N) away from the centre and weight (mg).
|
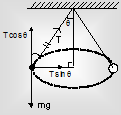
CONICAL PENDULUM: A small block of mass m is rotated in a horizontal circle with the help of a string of length connected to m. The other end of the string is fixed to a point O vertically above the centre of the circle so that the spring is usually inclined with the vertical at angleq. This arrangement is called as a conical pendulum.
From the force figure of the block:
|
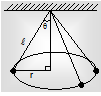 |
Along the vertical: T cosΘ = mg ... (1)
Net force towards centre: T sinΘ = ma
T sinΘ = m w2 r ... (2)
|
From (I) and (II), we have,
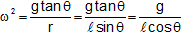
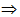 time period = time period =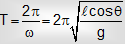
|
|
Note: 1) If the height of point O above the centre of the circle is h, then time period = 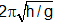
2) For a conical pendulum,
w2lcos =g 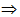
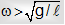 (Because cosΘ < 1)
(Because cosΘ < 1)
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Dynamics of Circular motion questions? Dynamics of Circular motion topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Dynamics of Circular motion related problems. We provide step by step Dynamics of Circular motion question's answers with 100% plagiarism free content. We prepare quality content and notes for Dynamics of Circular motion topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours