Digital filter design-The Butterworth filter:

Before going up design we produce below some of the substance relating filter descriptions to the filter order and the cut-off frequency.

A type of magnitude response specification is given below. The magnitudes at the critical frequencies Ω₁ and Ω₂ are A and B, respectively. For explaining  purposes we have

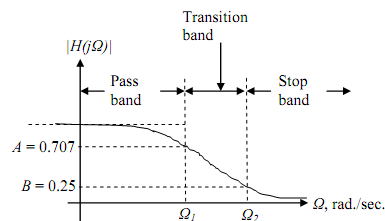
arbitrarily taken A = 0.707 (thus Ω1 is the cut-off frequency, but that need not be the case) and B = 0.25.

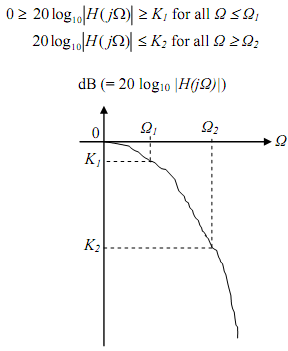
The log-magnitude specification is given below. Note that (20 log A) = K₁ and (20 log B) = K₂. Thus the analog filter needs are

With the resultant magnitude |H(jΩ)| shown by the Butterworth function,

and using the equality condition at the critical frequencies in the given specifications the order, N, of the filter is shown by

The result is circulated to the next larger integer. For example, if N = 3.2 by the above computation then it is related up to 4, and the order of the needed filter is N = 4. In that a case the resulting filter could exceed the specification at both Ω₁ and Ω₂. The cut-off frequency Ω_c is calculated from one of the two equations below.

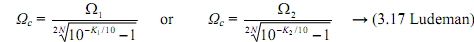
The equation on the left will result in the properties being met similarly at Ω₁ while the specification is preceded at Ω₂. The equation on the right results in the specification being collected exactly at Ω₂ and exceeded at Ω₁.

Example Realize a digital low pass filter taking the bilinear transformation function to satisfy the following characteristics:

(a) A monotonic pass band and stop band

(b) -3.01 dB cut off frequency of 0.5p rad.

(c) Magnitude down at least 15 dB at 0.75p rad.

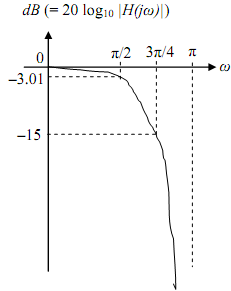
Note that the given frequencies are digital frequencies. The required frequency response is shown. We use bilinear transformation on an analog prototype.

Step 1 Pre-warp the critical digital frequencies ω₁ = 0.5p and ω₂ = 0.75p using T = 1 sec. That is, we find the analog frequencies ω´₁ and ω´₂ that correspond to ω₁ and ω₂:

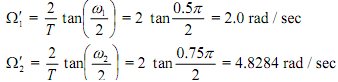
Step 2 Design LP analog filter with critical frequencies ω₁ and ω₂  that satisfy

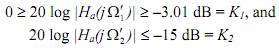
The Butterworth filter satisfies the monotonic property and has an order N and critical frequency Ω_c determined by Eq. 3.16 and 3.17 of Ludeman

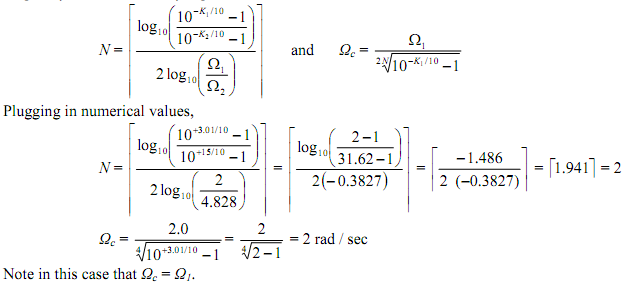
Therefore, the needed pre-warped, unit bandwidth, normalized, analog filter of order 2 using the Butterworth Table 3.1b (or the Butterworth circle) is

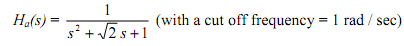 (with a cut off frequency = 1 rad / sec)

Since we need a cut-off frequency of Ω_c = 2 rad/sec, we next need the low pass to low pass transformation s → s/2 in order to take the cut-off frequency from 1 to 2 rad/sec.

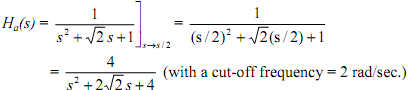 (with a cut-off frequency = 2 rad/sec.)

Step 3 Operating the bilinear transformation to Ha(s) with T = 1 will transform the pre-warped analog filter into a digital filter with the system function H(z) that can satisfy the provided digital requirements:

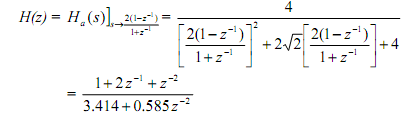
HW: calculate the difference equation. Plot | H (e^jΩ) | and ∠H (e jw ) vs ω.

Email based Digital filter design-The Butterworth filter assignment help - Digital filter design-The Butterworth filter homework help at Expertsmind

Are you finding answers for Digital filter design-The Butterworth filter based questions? Ask Digital filter design-The Butterworth filter questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Digital filter design-The Butterworth filter assignment help -Digital filter design-The Butterworth filter homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours