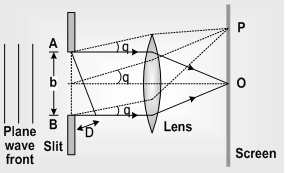
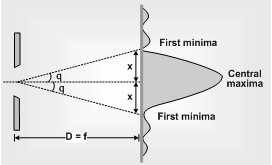
|
Suppose a plane wave front is incident on a slit AB (of width b). Each and every part of the expose part of the plane wave front (i.e. every part of the slit) acts as a source of secondary wavelets spreading in all directions. The diffraction is obtained on a screen placed at a large distance. (In practice, this condition is achieved by placing the screen at the focal plane of a converging lens placed just after the slit).
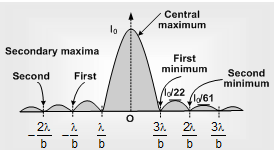
1. The diffraction pattern consists of a central bright fringe (central maxima) surrounded by dark and bright lines (called secondary minima and maxima).
|
|
2. At point O on the screen, the central maxima is obtained. The wavelets originating from points A and B meets in the same phase at this point, hence at O, intensity is maximum.
3. Secondary minima: For obtaining nth secondary minima at P on the screen, path difference between the diffracted waves Δ = bsinθ = nλ
(i) Angular position of nth secondary minima sinθ ≈ θ =nλ/b
(ii) Distance of nth secondary minima from central maxima
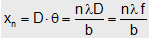; Where D = Distance between slit and screen. f≈D = Focal length of converging lens.
4. Secondary maxima : For nth secondary maxima at P on the screen
Path difference Δ = bsinθ = (2n+1)λ/2 ; n = 1, 2, 3, 4 .......
(i) Angular position of nth secondary maxima, sinθ ≈ θ = (2n+1)λ/2b
(ii) Distance of nth secondary maxima from central maxima,
|
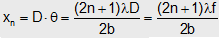
5. Central maxima: The central maxima lie between the first minima on both sides.
(i) The Angular width d central maxima = 2θ = 2λ/b
(ii) Linear width of central maxima
|
|
|
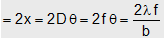
6. Intensity distribution: If the intensity of the central maxima is Io then the intensity of the first and second secondary maxima are found to be Io/22 and Io/61 . Thus diffraction fringes are of unequal width and unequal intensities.
(i) The mathematical expression for in intensity distribution on the screen is given by
|
|
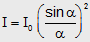Where a is just an interaction between the angle θ that locates a point on the viewing screening and light intensityI.
Φ = Phase difference between the bottom and top ray from the slit width b.
Also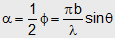 
(ii) As the slit width increases (relative to wavelength) the width of the control diffraction maxima decreases; that is, the wave undergoes less flaring by the road. The secondary maxima also decrease in width (and become weaker).
(iii) If b > > λ, the secondary maxima due to the slit disappear; we then no longer have single slit diffraction.
|
(iv) When the slit width is reduced by a factor of 2, the amplitude of the wave at the centre of the screen is reduced by a factor of 2, so the intensity at the centre is reduced by a factor of 4.
|
|
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Diffraction at single slit questions? Diffraction at single slit topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Diffraction at single slit related problems. We provide step by step Diffraction at single slit question's answers with 100% plagiarism free content. We prepare quality content and notes for Diffraction at single slit topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours