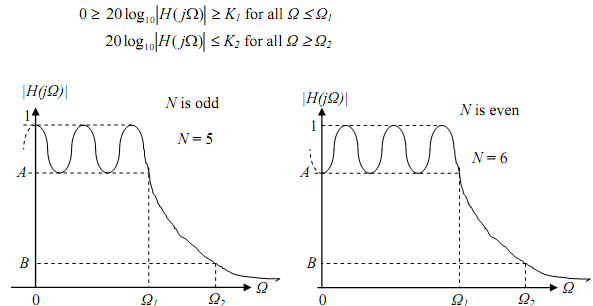
Design of the Chebyshev I filter A typical valuable response specification is given below (shown for N = 5 and N = 6). The magnitudes at the critical frequencies Ω1 and Ω2 are A and B, respectively. Typically Ω1 is in the pass band or is the edge of the pass band and Ω2 is in the stop band or is the edge of the stop band. In relates of the log-magnitude the analog filter specifications are as below. Note that (20 log A) = K1 dB and (20 log B) = K2 dB. If A and B are less than 1, K1 and K2 are negative.

The magnitude operation of the Nth order Chebyshev I filter is provided by

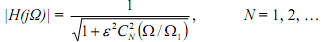
where ε has to do with pass band ripple and CN(x) is the Nth order Chebyshev cosine polynomial shown as

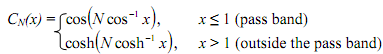
Chebyshev polynomials are also defined by the recursion formula

C_N ( x) = 2xC_{N -1} (x) - C_{N -2} (x)

with C₀ ( x) =1 and C₁ ( x) = x. Using this recursion formula we get, for N = 2, C₂ ( x) = 2.2xC₁ (x) - C₀ (x) = 2x² - 1.

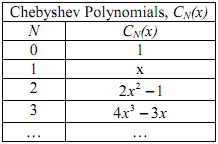
[Aside If the frequencies are normalized, that is, for a normalized filter, Ω₁ = 1 rad/sec and the value characteristic of the N^th order Chebyshev I filter is provided by

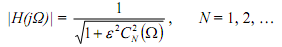
End of Aside]

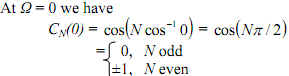
As a consequence, on the vertical axis (Ω = 0) the magnitude curve starts at |H(j0)| = 1 for odd N and at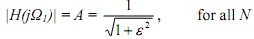 

At Ω = Ω₁ we have C_N(1) = cos(N cos ^-11) = cos(0) = 1 for all N. The related magnitude is

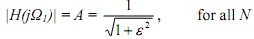
This equation is needed to calculate ε from the provided |H(jΩ)|.

The order, N, of the filter is provided by

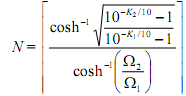
The symbol || seems that the calculated result is rounded to the next larger integer. For example, if N = 3.2 by the above computation then it is rounded up to 4, and the order of the needed filter is N = 4. In such a type the resulting filter could exceed the specification at both Ω₁ and Ω₂.

Email based Design of the Chebyshev assignment help - Design of the Chebyshev homework help at Expertsmind

Are you finding answers for Design of the Chebyshev based questions? Ask Design of the Chebyshev questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Design of the Chebyshev assignment help -Design of the Chebyshev homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours