Derivations and Context-Free Languages:

The productions of a grammar are used to generate strings. In this process, the productions are used as rewrite the rules.  

Formally, we define the derivation relation associated with the context-free grammar.  First, let us review the concepts of transitive closure and refiexive and transitive closure of the binary relation. Given a set A, of a binary relation R on A is any set of ordered pairs, that is R ⊆ A × A. For short, instead of binary relation, we simply say relation. Given any 2 relations R, S on A, their composition R o S can be defined as

RoS = {(x, y) ∈ A × A | ∃z ∈ A, (x,  z) ∈ R and (z, y) ∈ S}.

The identity relation I_A on A is relation I_A defined as

I_A = {(x, x) | x ∈ A}.

For short, we denote I_A as I . Keep in mind that

R o I = I o R = R

for every relation R on A. Given a relation R on A, for any n ≥ 0 we define Rn as shown below:

R⁰  = I,

Rⁿ⁺¹ = Rⁿ o R.

It is certain that R¹= R.  It is easily verified by induction that Rⁿ o R = R o Rⁿ . The transitive closure R+ of relation R can be defined as

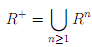
It is verified easily that R+  is the smallest transitive relation containing R, and that (x, y) ∈ R+ i there is n ≥ 1 and x₀ , x₁ ,..., x_n ∈ A such that x₀   = x, x_n = y, and (x_i , x_i+1 ) ∈ R  for all i, 0 ≤ i ≤ n - 1.  The transitive and refiexive closure R∗  of relation R can be defined as

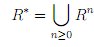
Evidently, R* = R+ ∪ I . It is verified easily that R∗ is the smallest transitive and refiexive relation containing R.

Definition: Given a context-free grammar G = (V, Σ, P, S), the derivation relation ⇒G  associated with G is binary relation ⇒G ⊆ V ∗ × V ∗ defined as follows: for all the α, β ∈ V ∗, we have

α ⇒G β

If there exist λ, ρ ∈ V*, and some production (A → γ) ∈ P , so that

α = λAρ     and  β = λγρ.

The transitive closure of ⇒G denoted as 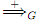and the refiexive and transitive closure of ⇒G  is denoted as.

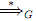When the grammar G is clear from the context, we usually omit the subscript G in ⇒G 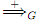 and ,

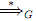A string α ∈ V* such that S 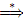α is called as sentential form, and a string ω∈ Σ∗ such that S  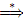ω is called a sentence.  A derivation α  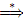β  involving n steps is denoted as α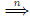β.

Note that a derivation step

α⇒Gβ

is nondeterministic.  Certainly, one can choose among various occurrences of nonterminals A in α, and among various productions A → γ with left hand side A.

For instance, using the grammar G₁  = ({E, a, b}, {a, b}, P, E), here P is the set of rules

E -→ aEb,

E -→ ab,

every derivation from E is of form

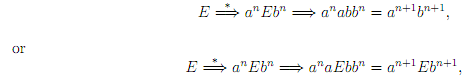
here n ≥ 0.

Grammar G₁ is simple: every string aⁿ bⁿ  posses a unique derivation.  This is generally not the case. For instance, using the grammar G₂  = ({E, +, ∗, (, ), a}, {+, ∗, (, ), a}, P, E), here P is the set of rules

E -→ E + E,

E -→ E ∗ E,

E -→ (E),

E -→ a,

the string a + a ∗ a has distinct derivations which are stated as follows, where the boldface indicates which occurrence of E can be rewritten:

E ⇒ E ∗ E ⇒ E + E ∗ E

⇒ a + E ∗ E ⇒ a + a ∗ E ⇒ a + a ∗ a,

and

E ⇒ E + E ⇒ a + E

⇒ a + E ∗ E⇒ a + a ∗ E ⇒ a + a ∗ a.

In the above derivations, the leftmost occurrence of the nonterminal is chosen at each step. This type of derivations is known as leftmost derivations. Rewrite the right occurrence of the nonterminal, getting the rightmost derivations.  The string a + a ∗ a also has the 2 rightmost derivations stated below, where the boldface indicates which occurrence of E can be rewritten:

E ⇒ E + E ⇒ E + E ∗ E

⇒ E + E ∗ a ⇒ E + a ∗ a ⇒ a + a ∗ a,

and

E ⇒ E ∗ E ⇒ E ∗ a

⇒ E + E ∗ a ⇒ E + a ∗ a ⇒ a + a ∗ a.

The language generated by the context-free grammar can be defined as follows.

Email based Automata assignment help - homework help

The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help - Automata homework help and online tutoring with best qualified and experienced computer science tutor's help. We cover all topics including Derivations and Context-Free Languages in assignment help - homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.