Definite integral as limit of a sum:

An alternative way of describing 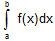 is that the definite integral 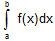is a limiting case of the summation of an infinite series, provided f(x) is continuous on [a, b] that is  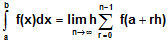where h = b-a/n. The converse is true that is, if we have an infinite series of the above form, it is expressed as a definite integral.

Method to express infinite series as definite integral:

(i) Express given series in the form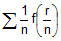 

(ii) Then limit is its sum when n->∞, i.e.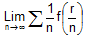 

(iii) Replace r/n by x and 1/n by dx and 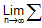by the sign of ∫.

(iv) The lower and upper limit of integration are limiting values of r/n for the 1^st and the last term of r respectively.

Some of the particular cases of the above are given below

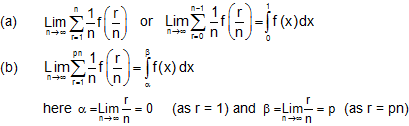
Illustration:  Show that

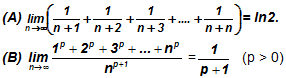
Solution:             (A) Let  I =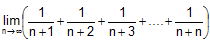  

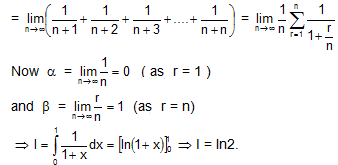
                              (B)            

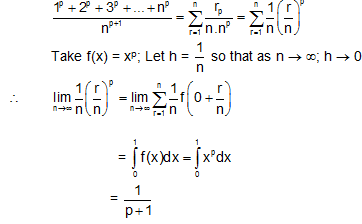
Email based Definite integral as limit of a sum Assignment Help - Homework Help

We at www.expertsmind.com offer email based Definite integral as limit of a sum assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.

Expertsmind's best education services

• Quality assignment-homework help assistance 24x7 hrs
• Best qualified tutor's network
• Time on delivery
• Quality assurance before delivery
• 100% originality and fresh work