FA M, L(M) is a regular language

Proof: Let M = (Q, ∑, δ, q1, F) be an FA, where Q={qi| 1 ≤ i ≤ n} for some positive integer n.

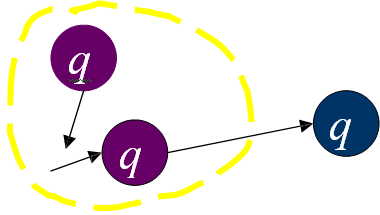
Suppose R(i, j, k) be the set of all strings in the drive M from state qi to state qj while passing through any state ql , for l ≤ k. (i and j can be any states)

We prove that L(M) is the regular language by illustrating that there is a usual expression consequent to L(M), by induction.

Basis: R(i, j, 0) corresponds to a regular expression a if i≠ j and a + ε if i= j for some a∑∈.

Induction hypotheses: Suppose R(i, j,k-1) correspond to a usual expression, for any i, j, k≤n.

Induction step: 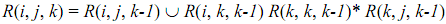 corresponds to a regular expression as R(i, j, k-1), R(i, k, k-1), R(k, k, k-1) and R(k, j, k-1) correspond to some regular expressions and union, concatenation, and Kleene's star are permitted in regular expressions. Therefore, L(M) is a regular language as L(M) = + R(1, f, n) for all qf in F.

Email based Automata assignment help - homework help

The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help - Automata homework help and online tutoring with best qualified and experienced computer science tutor's help. We cover all topics including Define a regular language for a FA in assignment help - homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.