Define a context-free language:

Given a context-free grammar G = (V, Σ, P, S), the language generated by G is the set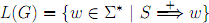 

A language L  ⊆ Σ*  is a context-free language if L  = L(G) for some context-free grammar G.

It is technically quite useful to consider derivations in which the leftmost nonterminal is selected always for rewriting, derivations in which the rightmost nonterminal is selected always for rewriting.

Definition:  Given the context-free grammar G = (V, Σ, P, S), the leftmost derivation relation 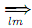 associated with G is the binary relation  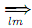⊆ V* × V*  de?ned as follows: for all α, β ∈ V*, we have

α 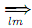   β

if there exist u ∈ Σ*, ρ ∈ V*, and some production  (A → γ) ∈ P , so that

α = uAρ     and  β = uγρ.

The transitive closure of 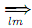 is denoted as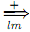and the transitive and re?exive closure of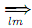is denoted as 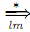. The (one-step) rightmost derivation relation  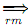related with G is the binary relation 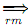⊆ V*× V* de?ned as follows: for all α, β ∈ V*, we have

α 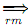  β

iff there exist λ ∈ V*, v ∈ Σ*, and some production  (A → γ) ∈ P , so that

α = λAv     and  β = λγv.

The transitive closure of 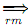 is denoted as  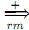and the reflexive and transitive closure of  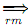is denoted as .

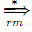Remarks:  It is compulsory to use the symbols a, b, c, d, e for terminal symbols, and symbols A, B, C, D, E for nonterminal symbols. The symbols u, v, w, x, y, z denote terminal strings, and the symbols α, β, γ, λ, ρ, µ denote strings in V*. The symbols X, Y, Z generally denote symbols in V .

Given a context-free grammar G = (V, Σ, P, S), parsing a string w consists in finding out whether ω ∈ L(G), and if so, in generating a derivation for ω.  The following lemma is technically significant. It shows that leftmost and rightmost derivations are "universal". This has significant practical implications for complication of the parsing algorithms.

Lemma: Let G  = (V, Σ, P, S) be the context free grammar. For each ω ∈ Σ*, for every derivation S 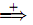ω, there is a leftmost derivation S 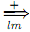ω, and there is a rightmost derivation S  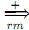ω.

Proof . Certainly, we have to use induction on derivations, although this is a bit tricky, and it is essential to prove a stronger fact.

Claim: For every w ∈ Σ*, for every α ∈ V⁺, for every n ≥ 1, if α 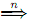 ω, then there is a lef tmost derivation α  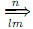ω.

The can be proved by induction on n.

For n = 1, there exist λ, ρ ∈ V* and production  A → γ, such that α = λAρ and ω = λγρ. As w is a terminal string, λ, ρ, and γ, are the terminal strings. Therfore, A is the only nonterminal in α, and the derivation step α 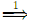 ω is a leftmost step (and a rightmost  step!).

If n > 1, then the derivation α 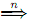 ω is of the form

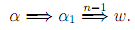
There are 2 subcases.

Case1. If the derivation step α = α1 is a leftmost step α 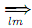 α1 , by induction hypothesis, there is a leftmost derivation α1  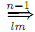ω, and we get leftmost derivation

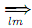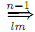α α₁ ω

Case 2. The derivation step α ⇒ α1   is a not a leftmost step. In this case, there should be some u ∈ Σ*, µ, ρ ∈ V*, some nonterminals  A and B, and some production  B → δ, such that

where A is the leftmost nonterminal in α.  As we have a derivation  α1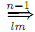w , by the induction hypothesis, there is a leftmost derivation ω of length

α₁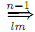 ω

Since α1   = uAµδρ  where A  is the leftmost terminal in α1 , the 1st step in the leftmost derivation α1 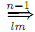 ω is of the form

uAµδρ  => uγµδρ,

for some production A → γ. Therefore, we have a derivation of the form

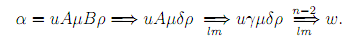
We can commute the 1st 2 steps involving the productions B  → δ and A → γ, and we get the derivation

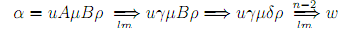
This may no longer be a leftmost derivation, but the 1st step is leftmost, and we are back in case 1. Therefore, we conclude by applying the induction hypothesis to the derivation uγµBρ 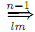 ω, as in case 1.

Email based Automata assignment help - homework help

The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help - Automata homework help and online tutoring with best qualified and experienced computer science tutor's help. We cover all topics including Define a context-free language in assignment help - homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.