Context-Free Languages as  Least Fixed-Points:

Given a context-free grammar G = (V, Σ, P, S) with m nonterminals A₁ ,... A_m, grouping all the productions having same left-hand side, the grammar G can be written as

A₁  → α₁,₁  + ··· + α₁,n₁ ,

··· → ··· 

A_i → α_i,₁  + ··· + α_i,n_i ,

··· → ··· 

A_m → α_m,₁ + ··· + α_m,n_n .

Given any set A, let P_fin (A) be the set of finite subsets of A.

Definition: Let G = (V, Σ, P, S) be a context-free grammar with m nonterminals A₁ , .. ., Am. For any m-tuple Λ = (L₁ ,..., L_m) of languages L_i ⊆ Σ*, we define the function

inductively as stated:

Φ[Λ](∅)= ∅,

Φ[Λ]({ })= { },

Φ[Λ]({a})= {a},       if a ∈ Σ,

Φ[Λ]({A_i })= L_i,       if A_i ∈ N ,

Φ[Λ]({αX })= Φ[Λ]({α})Φ[Λ]({X }),         if α ∈ V⁺, X ∈ V,

Φ[Λ](Q ∪ {α})= Φ[Λ](Q) ∪ Φ[Λ]({α}),        if Q ∈ P_fin (V ∗), Q = ∅, α ∈ V*, α ∈/ Q.

Then, writing grammar G as follows

A₁  → α₁,₁  + ··· + α₁,n₁ ,

··· → ··· 

A_i → α_i,₁  + ··· + α_i,n_i ,

··· → ··· 

A_m → α_m,₁ + ··· + α_m,n_n .

we may define the map

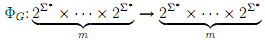
so that

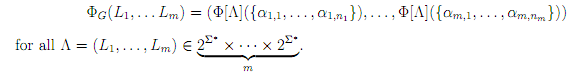
One should verify that map Φ[Λ] is well defined, but this is simple. The following lemma is shown easily:

Lemma: Given a context-free grammar G = (V, Σ, P, S) with m nonterminals A₁ , .. ., A_m, map

is ω-continuous.

Now, 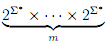 is an ω-chain complete poset, and map Φ_G is ω-continous. Thus, by lemma, the map Φ_G has a least-fixed point.  It turns out that the components of this least fixed-point are precisely the languages generated by the grammars (V, Σ, P, Ai ). Before giving this fact, there is an example explaning  it.

Example. Consider the grammar G = ({A, B, a, b}, {a, b}, P, A) can be defined by the rules

A → BB  + ab,

B → aBb + ab.

The least fixed-point of Φ_G is least upper bound of the chain

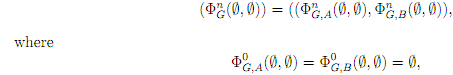
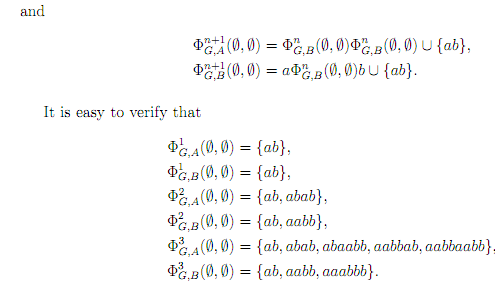
By induction, we can prove that the 2 components of the least fixed-point are the languages

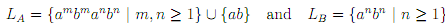
Letting G_A  = ({A, B, a, b}, {a, b}, P, A) and G_B = ({A, B, a, b}, {a, b}, P, B), it is indeed true that L_A = L(G_A) and L_B  = L(G_B).

Email based Automata assignment help - homework help

The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help - Automata homework help and online tutoring with best qualified and experienced computer science tutor's help. We cover all topics including Context-Free Languages as Least Fixed-Points in assignment help - homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.