Conjugate hyperbola:

The hyperbola, whose transverse and conjugate axes are the conjugate and transverse axes of a given hyperbola respectively, is called as conjugate hyperbola of the given hyperbola, and the 2 hyperbolas are conjugate to one another. Therefore, the hyperbolas 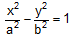 and 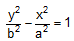 are the conjugate hyperbolas.

Illustration: Tangents are drawn to the hyperbola from any point on one of the branches of conjugate hyperbola. Show that their chord of contact will touch other branch of conjugate hyperbola.

Solution: Let the hyperbola be 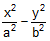 = 1. So the conjugate hyperbola is  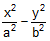= - 1. Let any point on it be (a tanθ, b secθ). Now the equation of chord of contact will be

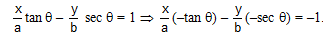
So, it is a tangent to conjugate hyperbola at the point (- a tanθ, - b secθ) which will obviously on other branch. 

Email based Conjugate hyperbola Assignment Help -Conjugate hyperbola Homework Help

We at www.expertsmind.com offer email based Conjugate hyperbola assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.

Expertsmind's best education services

• Quality assignment-homework help assistance 24x7 hrs
• Best qualified tutor's network
• Time on delivery
• Quality assurance before delivery
• 100% originality and fresh work