Conductivity and Mobility

• Even at the thermal equilibrium, the carriers are constantly in motion within the lattice.
• At room temperature, the thermal motion of an individual electron can be visualized as random scattering from lattice impurities, atoms, other electrons, and defects.
• There is no net motion of group of n eletrons/cm³ over any period of time, since the scattering is random, and there is no preferred direction of motion for group of electrons and no net current flow.
• Although, for an individual electron, this is not true the probability of an electron returning to its initial point after time t is negligibly small.
• Now, if the electric field E_x is applied in x-direction, each electron experiences a net force q E_x from field.
• This will generate a net motion of group in the x-direction, even though the force may be insufficient to appreciably alter the random path of an individual electron.
• If p_x is the x-component of the total momentum of the group, then the force of the field on the n  eletrons/cm³ is

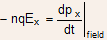                  (2.18)

Note: this expression indicates a constant acceleration in x-direction, which cannot happen actually.

• In steady state, this acceleration is balanced by the deceleration because of the collisions.
• Thus, while the steady field   E_x produce a net momentum P - x, for steady state current flow, the net rate of change of momentum should be zero when collisions are included.

• Note: the collision processes are entirely random, thus, there is a constant probability of collision at any time for each of the electron.
• Consider a group of N₀ electrons at time t = 0, and define N(t) as number of electrons which have not undergone a collision by time t

Figure- The random thermal motion can be seen of an individual electron, undergoing random scattering.

• The rate of decrease of N(t) at any time t is proportional to the number left unscattered at t, that is

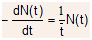                           (2.19)

here 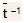   is constant of proportionality.

• The solution is an exponential function which is given as follows

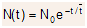                   (2.20)

and 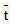   represents the mean time in between scattering events, called as mean free time.

• The possibility that any electron has a collision in time interval dt is dt/ 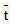  , thus, the differential change in                        because of collisions in time dt is

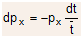           (2.21)

• Thus, the rate of change of because of the decelerating effect of collisions is

                      (2.22)

• For steady state, the sum of acceleration and deceleration effects should be zero, thus,   (2.23)

• The average momentum per electron (averaged over the whole group of electrons) is

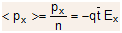                     (2.24)

• Thus, as expected for the steady state, electrons would have on the average a constant net velocity in x direction

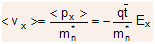(2.25)

• This speed is referred to as drift speed, and, generally it is much smaller than the random speed because of thermal motion  .

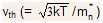• The current density resulting from this drift velocity

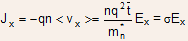       (2.26)

• This is familiar Ohm's law with 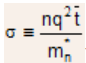     being conductivity of the sample, this can  also  be  written  as  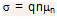   ,  with  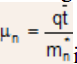   is  defined  as  electron  mobility (in   cm²/V-Sec),  and  it  describes the ease  with  which the electrons drift  in  material.

• The mobility can also be expressed in terms of average drift velocity per unit electric field, therefore  with the negative sign denoting the positive value for mobility since electrons drift opposite to the direction of electric field.

• The total current density can be given as   (2.27) when electrons and holes both contribute to the current conduction; on the other hand, for predominantly n type or p type samples, the first or the second term of the equation stated above dominates.

Note: electron and hole both drift currents are in same direction, since holes (having positive charges) move along the direction of the electric field, and electrons (having negative charges) drift opposite to the direction of electric field.

• As GaAs has a strong curvature of E-k diagram at bottom of the conduction band, the electron effective mass in the GaAs is very small    the electron mobility in GaAs is quite high since μ_n is inversely proportional to    .
• The other parameter in mobility expression, that is, 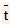  (the mean free time between the collisions) is a function of temperature and the impurity concentration in semiconductor.

• For the uniformly doped semiconductor bar of length L, thickness t, and width w, the resistance R of the bar can be given by 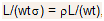  here Ρ is the resistivity.

Email based Digital Electronics assignment help - homework help at Expertsmind

Are you searching Electronics Engineering assignment help expert for help with Conductivity and Mobility questions?  Conductivity and Mobility topic is not easier to learn without any external help?  We at www.expertsmind.com offers free lecture notes for Digital Electronics assignment help and Digital Electronics homework help. Live tutors are available 24x7 hours for helping students in their Conductivity and Mobility related problems. We provide step by step Conductivity and Mobility question's answers with 100% plagiarism free content. We prepare quality content and notes for Conductivity and Mobility topic under digital electronics theory and study material. These are avail for subscribed users and they can get advantages anytime.

Why Expertsmind for assignment help

1. Higher degree holder and experienced experts network
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. Time on Delivery
5. Privacy of information and details
6. Excellence in solving electronics engineering questions in excels and word format.
7. Best tutoring assistance 24x7 hours