Computation of frequency response
Let the system function be given by the following equation
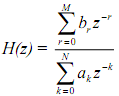
The frequency response is H (e jw ) or H(ω) = H (z)z = e jw . Therefore
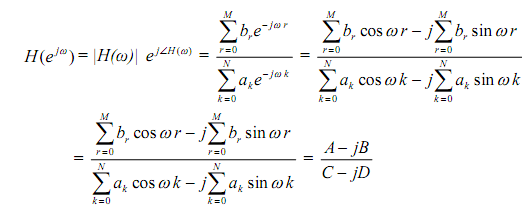
where
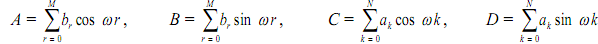
The magnitude and phase of H (ejw ) are given, by
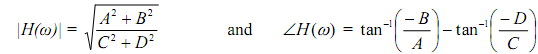
Theorem The frequency response H (e jw ) for the BIBO-stable system will always converge.
Accordingly every BIBO-stable system will have the frequency response and the describable steady- state response to sinusoidal inputs. But, converse of this statement is not true, which means that the fact that H (e jw ) exists does not imply that the system is stable.
Example The ideal low pass filter
For the H(ω) given in the figure drawn below find out h(n), the unit sample response.
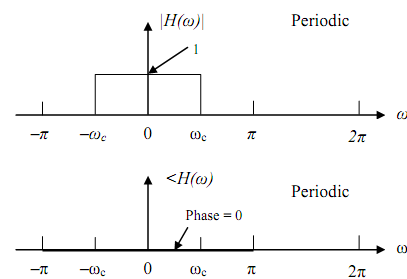
Solution The unit sample response is inverse DTFT of H(ω)
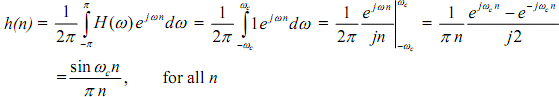
It is seen that h(n) ≠ 0 for negative n so that the ideal low pass filter is noncausal. Furthermore, 
h(n) tails off as n goes from 0 to ∞ and from 0 to -∞, it can be shown that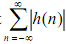 
not finite. This shows that ideal low pass filter is not BIBO-stable either.
Email based Computation of frequency response assignment help - Computation of frequency response homework help at Expertsmind
Are you finding answers for Computation of frequency response based questions? Ask Computation of frequency response questions and get answers from qualified and experienced Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Computation of frequency response assignment help -Computation of frequency response homework help and Digital signal processing problem's solution with step by step procedure.
Why Expertsmind for Digital signal processing assignment help service
1. higher degree holder and experienced tutors
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. On Time Delivery
5. Privacy of information and details
6. Excellence in solving Digital signal processing queries in excels and word format.
7. Best tutoring assistance 24x7 hours