Composition of two simple harmonic motions at right angles to each other Lissajous' figures.
Imagine a simple pendulum suspended from a stand placed in a boat and set into simple harmonic vibrations along the directions of the length of the boat. Let the boat also toss sideways. The bob of the pendulum is now under the influence of two simple harmonic vibrations - its own along the directions of the length of the boat and another in a direction perpendicular to this due to the tossing of the boat. As a consequence the bob in this case moves along the direction of the resultant of these two simple harmonic motions and describes a curve known as Lissajous; figures. The Lissajous' figure may thus be described as a curve which represents the resultant of two simple harmonic vibrations at right angles to each other. The actual shape of the curve depends upon the relative periodic times, amplitude and phase of two component vibrations.
The resultant of two simple harmonic motions at right angles to each other may be obtained by any of the two methods, viz., (i) graphic method and (ii) Analytical method.
GRAPHIC METHOD FOR GETTING THE RESULTANT OF TWO simple harmonic MOTIONS AT RIGHT ANGLES TO EACH OTHER
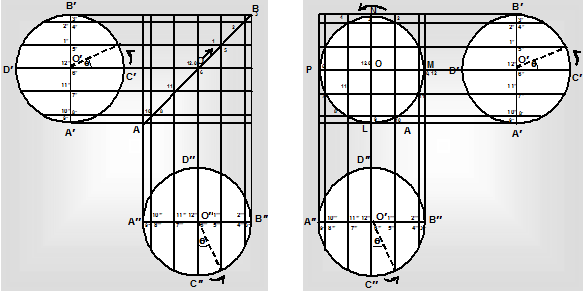
(i) When they have the same periodic time, equal amplitudes and no phase difference: Let the two simple harmonic motions occur along two perpendicular directions A"B" and A'B' represented in figure. Let A'B'C'D' with centre O' and A"B"C"D" with centre O" be their respective circles of reference. Since the two vibrations have equal amplitudes, the two circles will have equal radii. Divide the circumference of each circle into 12 equal parts and from each point of divisions, draw a perpendicular on the respective diameters A'B' or A"B" and produce it as shown in the figure. Since there is no phase difference between the two simple harmonic motions, the starting positions of the component motion may be represented by O' and O" on the two diameters' A'O'B' and A"O"B". The resultant starting position is represented by O, the point of intersection of the perpendiculars on A'B' and A"B" at the points O' and O". The points of intersection of the perpendiculars on A'B' and A"B" viz., 1, 2, 3 . . . . . . . 12, represent the resultant positions of the particle having the two simple harmonic motions after intervals of . The curve obtained by joining these points gives the resultant path of the particle which, in this case, will be seen to be a straight line inclined at 45° to the direction of the component vibrations.
(ii) When the two simple harmonic motions have the same periodic time, equal amplitudes and a phase difference = : The resultant curve may be obtained in this case in the same manner as in (i) above. While the starting point for one S.H.M. is O', the starting point of the other is B"; the phase difference between these two being . The starting point of resultant is M. see in figure. As clear from the figure, the resultant curve or the Lissajou's figure will be a circle in this case.
|
(iii) When the two simple harmonic motions have the same periodic time but different amplitude and a phase difference = p/2: The resultant curve may be obtained graphically as above. Since the two vibrations have different amplitudes, the radii of the two component circles will be different in this case. The resultant will be an ellipse with axes along the
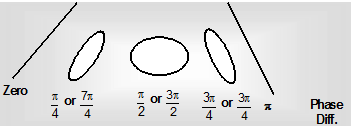
direction of the component vibrations.
|
|
(iv) When the two simple harmonic motions have different amplitudes and also differ in phase but they have the same periodic time : The resultant curve may be obtained graphically in the above manner. Its shape will be found to differ with different phase differences as shown in figure. It is to be noted that the resultant value' figure in this case is generally an ellipse, the eccentricity and the inclination of which depend on the two amplitudes and the phase difference. When the phase difference is zero or p, the ellipse changes to a straight line.
(v) When the component simple harmonic motions have different periodic times: The resultant curve may be obtained in this case by dividing the circumferences of the two circles of reference into parts in the ratio of the periodic times, so that the projections of the parts on respective diameters give the displacements due to the individual simple harmonic motions in equal intervals of time.
- The slope of the tangent drawn on the U versus X graph gives us the value of the restoring force acting on the block.
- The graph can be used to obtain the value of PE stored in the spring at any stage.
- If we place a small ball in the U versus X graph then oscillatory motion of the ball will help us in understanding the motion of the block.
- We can use this graph to find out the total energy of the oscillating system.
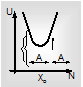
- Consider the U versus X graph to be is given as
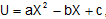 where a > 0. If a particle of mass M oscillates in this potential field then we have to find out the time period and analyze the motion.
where a > 0. If a particle of mass M oscillates in this potential field then we have to find out the time period and analyze the motion.
In such a phase, first of all you have to find out the equilibrium position by setting dU/dX =0 we get, X0 = -b//2a to be the stable equilibrium.
We also know that 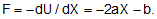
The displacement from the mean position is X- X2 Let us writing 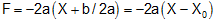 Hence, the force constant of the system is "2a". (This is equivalent to the spring constant). The time period of oscillation will be equal to
Hence, the force constant of the system is "2a". (This is equivalent to the spring constant). The time period of oscillation will be equal to 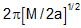
- In the above example, if the body oscillates between
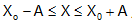 , then find out the energy of oscillation. Observe the graph for better understanding. , then find out the energy of oscillation. Observe the graph for better understanding.
|
|
- Should realize that by shifting the parabola from the origin we do not change its original shape. The restoring force and the time period of oscillation depend on the shape of the parabola and not on its position in the coordinate plane. Students should also know that the shape of the parabola is decided by the coefficient of X2. Therefore, if any question is asked to get the time period, then we should only look at the value of 'a'.
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Composition of two simple harmonic motions questions? Composition of two simple harmonic motions topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Composition of two simple harmonic motions related problems. We provide step by step Composition of two simple harmonic motions question's answers with 100% plagiarism free content. We prepare quality content and notes for Composition of two simple harmonic motions topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours