Closure Properties of the Class of Recursively Enumerable Languages

Theorem:

Let L1 and L2 be recursively enumerable languages over ∑. Then, L1∪L2 is recursively enumerable.

Proof:

Let L1 and L2 be recursively enumerable languages over ∑.

Then, there is TM's T1 and T2 accepting L1 and L2, respectively.

Construct an NTM M as follows.

Closure Property Under Union

If w is in L1, but not in L2, then T1 in M runs and stops. If w is in not L1, but in L2, then T2 in M runs and stops.

If w is in both L1 and L2, then either T1 or T2 runs and stops. For these 3 cases, M halts.

If w is neither in L1 nor in L2, then either T1 or T2 runs but both never halt.  Then, M does not stop.

Therefore, M accepts L1∪L2. That is, L1∪L2 is enumerable recursively.

Closure Property Under Intersection

Theorem:

Let L1 and L2 be recursively enumerable languages over ∑. Then, L1∩L2 is also recursively enumerable.

Proof:

Let L1 and L2 be enumerable recursively languages over ∑.

Then, there exist TM's T1 and T2 accepting L1 and L2, respectively.

Construct an NTM M as follows.

→ TcopyTape1ToTape2 → T1 → TmoveRight  1 → TcopyTape2ToTape1 → T2

Closure Property Under Intersection

If w is in not L1, then T1 in M does not stop. Then, M does not halt.

If w is in L1, but not in L2, then T1 in M stop and  T2 can finally start, but does not stop. Then, M does not stop.

If w is in both L1 and L2, then T1 in M stops and T2 can finally begin, and finally stop. Then, M halts.

Therefore, M accepts L1∩L2. That is, L1∩L2 is recursively enumerable.

Closure Property Under Intersection (II)

Theorem:

Let L1 and L2 be enumerable recursive languages over ∑. Then, L1∩L2 is also recursively enumerable. 

Proof:

Let L1 and L2 be enumerable recursive languages over ∑.

Then, there is DTM's T1 = (Q1, Σ1, Γ1, δ1, s1)  and T2 = (Q2, Σ2, Γ2, δ2, s2)  accepting L1 and L2, respectively.

Construct a 2-tape TM M which simulates T1 and T2.  Tape 1 represents T1's tape and Tape 2 represents T2's tape.

Closure Property Under Intersection (II)

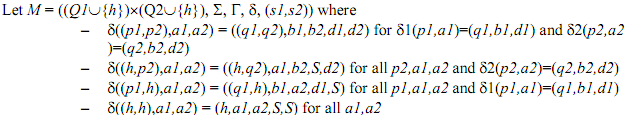
If neither T1 nor T2 halt, M never gets to the state h.

If T1 halts and T2 does not stop, M gets to the state (h,p).

If T2 stops and T1 does not stop, M gets to the state (p,h).

If both T1 and T2 halt, M finally gets to the state h.

Email based Automata assignment help - homework help

The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help - Automata homework help and online tutoring with best qualified and experienced computer science tutor's help. We cover all topics including Closure Properties of the Class of Recursively Enumerable Languages in assignment help - homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.