Closure Properties

• The class of languages accepted by FA's is closed under the operations

-     Union

-     Concatenation

-     Complementation

-     Kleene's star

-     Intersection

The class of languages accepted by FA is closed under union.

Proof:

Let MA = (QA, Σ, δA, sA, FA) and

MB = (QB, Σ, δB, sB, FB) be any FA. We construct an NFA M = 

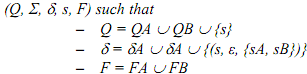
To prove L(M) = L(MA)∪L(MB), we prove:

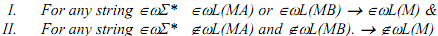
For I, consider (a) ∈ωL(MA) or (b) ∈ωL(MB).

For (a), let ∈ωL(MA).

From the definition of strings accepted by an FA, there is a state fA in FA such that (sA, ω) |-*M (fA, ε).

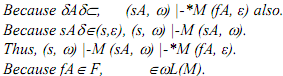
Similarly for (b).

For (II), let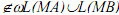 

Because (s, ε, {sA, sB})δ∈, either (s,w) |-M (sA,w) or (s, w) |-M (sB, w) only.

Because ∈wL(MA), there exists no fA in FA so that (sA,w) |-*MA (fA,ε). Because ∈wL(MB), there exists no fB in FB so that (sB, w) |-*MB (fB, ε).

As there is no transition between states in QA and QB in M, there is no state f in

F=FA∪FB such that (s, ω) |-M (sA, ω) |-*M (fA, ε) or (s, ω) |-M (sB, w) |-*M (fB, ε).

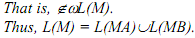
Closure under concatenation

The class of languages which is accepted by FA is closed under intersection.
Proof:
Let L1 and L2 be languages accepted by FA.

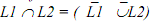
By closure property under complementation, there are FA accepting L1 and L2.
By closure property under union, there is an FA accepting.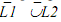

By closure property under complementation, there is an FA accepting(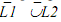). Therefore, the class of languages accepted by FA is closed under intersection.

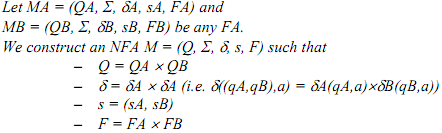
Email based Automata assignment help - homework help

The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help - Automata homework help and online tutoring with best qualified and experienced computer science tutor's help. We cover all topics including Closure Properties in assignment help - homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.