Classification of matrices:

Row Matrix:

A matrix contains a single row is known as a row matrix.  e. g.  [1  3  5  7]

Column Matrix:

A matrix contains a single column is known as a column matrix.  e.g. .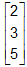 

Square Matrix:

An m x n matrix A is called be a square matrix if m = n i.e.  number of columns = number of rows.

As like: 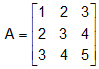  is a square matrix of order 3 x 3.

Note:       

• The diagonal from left hand side top corner to right hand side lower side lower corner is called as principal diagonal or leading diagonal. In the given example square matrix having the elements 1, 3, 5 is known as the principal diagonal or leading.

Trace of a Matrix:

The addition of the elements of a square matrix A lying along the principal diagonal is known as the trace of A i.e.  tr(A)

Therefore if A = [a_ij]_nxn

Then tr(A) = 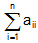 = a₁₁ + a₂₂ + ..... + a_nn

Problem:          calculate the trace of the matrix A = .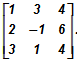

Solution:       tr (A) = 1 + (-1) + 4 = 4.

Diagonal Matrix:

A square matrix all of whose components except those in the leading diagonal, are zero is defined as a diagonal matrix. For a square matrix A = [a_ij]_nxn to be a diagonal matrix, a_ij = 0, whenever i ≠ j.

Problem: 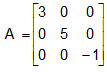  is a diagonal matrix of order 3 x 3.

Scalar Matrix:

A diagonal matrix whose each leading diagonal elements are same is known as a scalar matrix.

For a square matrix A = [a_ij]_nxn to be a scalar matrix a_ij = 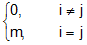, where m ≠ 0.

problem: 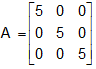  is a scalar matrix.

Unit Matrix or Identity Matrix:

A diagonal matrix of n^th order which has unity for all its diagonal components, is known as a unit matrix of order n and is shown by I_n.

Therefore a square matrix A = [a_ij]_nxn is a unit matrix if a_ij =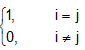 

problem:  

Triangular Matrix:

A square matrix in which all the components below the diagonal elements are zero is known as Upper Triangular matrix and a square matrix in which all the components above diagonal components are zero is known as Lower Triangular matrix.

Provided a square matrix A = [a_ij]_nxn,

For upper triangular matrix, a_ij = 0,            i > j

and for lower triangular matrix, a_ij = 0,  i < j

Notes:

• Diagonal matrix is both upper and lower triangular
• A triangular matrix A = [a_ij]_n´n is called as strictly triangular if a_ii = 0 for  1 ≤ i ≤ n.

For example: 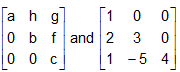are respectively upper and lower triangular matrices.

Null Matrix:

If each element of a matrix (square or rectangular) are zero, it is known as a null or zero matrix.

For A = [a_ij] to be null matrix, a_ij = 0  ∀ i, j

For example: 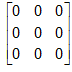  is a zero matrix

Email based Classification of matrices Assignment Help -Classification of matrices Homework Help

We at www.expertsmind.com offer email based Classification of matrices assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.

Expertsmind's best education services

• Quality assignment-homework help assistance 24x7 hrs
• Best qualified tutor's network
• Time on delivery
• Quality assurance before delivery
• 100% originality and fresh work