Circular permutations:
There are arrangements in enclosed loops also, known as circular arrangements.
Consider n persons (a1, a2, a3,...,an) are to be arranged about a circular table. The total number of circular arrangements of n persons is n!/n = (n - 1)!.
Distinction between anti-clockwise and clockwise Arrangements:
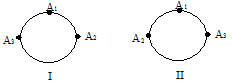
Suppose the subsequent circular arrangements:
|
In figure I, the order is clockwise whereas in figure II, the order is anti-clock wise. These are two distinct arrangements. When distinction is prepared between the anti-clockwise and the clockwise arrangements of n distinct objects around a circle, then the number of arrangements = (n - 1)!
|
|
But if no distinction is prepared between the clockwise and the anti-clockwise arrangements of n distinct objects about a circle, then the total number of arrangements is 1/2(n - 1)!
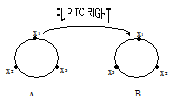
For an example, suppose the arrangements of beads (all different) on a necklace as given in figures B and A.
|
Look at (A) placing 3 beads x1, x2, x3 as define. Flip (A) over on its right. We obtain (B) at once. However, (A) and (B) are actually the outcomes of one arrangement but are numbered as two distinct arrangements in our computation. To nullify this redundancy, the normal number of different arrangements is (n-1)!/2.
|
|
Remarks:
When the related positions are numbered, circular arrangement is behaved as a linear arrangement.
In a linear arrangement, it does not create difference whether the position are numbered or not.
Example: Suppose 23 distinct coloured beads in a necklace. In how many various types may the beads be placed in the necklace so that 3 particular beads always remain together?
Solution: By theory, let us take 3 beads as one. Therefore we have, in effect, 21 beads, 'n' = 21. The number of arrangements = (n-1)! = 20!
Also, the number of paths in which 3 beads may be organized between themselves is 3! = 3 x 2 x 1 = 6.
Therefore the total number of arrangements = (1/2). 20!. 3!.
Example: In how many types 10 boys and 5 girls may sit around a circular table so that no two girls place together.
|
Solution: 10 boys may be placed in a circle in 9! ways. There are 10 spaces in between the boys, which will be placed by 5 girls in 10p5 ways. Therefore total number of types
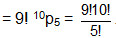
|
|
Email based Circular permutations Assignment Help -Circular permutations Homework Help
We at www.expertsmind.com offer email based Circular permutations assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.
Expertsmind's best education services
- Quality assignment-homework help assistance 24x7 hrs
- Best qualified tutor's network
- Time on delivery
- Quality assurance before delivery
- 100% originality and fresh work