Chomsky Normal Form:

One of the main aims of this section is to show that every CFG G can be changed to an equivalent grammar in Chomsky Normal Form. A context-free grammar

G = (V, Σ, P, S) is in Chomsky Normal Form iff its productions are of form

A → BC,

A → a,      or

S →  ∈,

where A, B, C  ∈ N , a ∈ Σ, S  →∈ is in P  iff ∈ L(G), and S  does not take place on the right-hand side of any production.

Note that a grammar in Chomsky Normal Form does not have  -rules, that is, rules of the form A → ∈, except when ∈ L(G), in which case S → ∈  is the only ∈-rule. It also does not have chain rules, i.e., rules of the form A → B, where A, B ∈ N . Thus, in order to convert a grammar to Chomsky Normal Form, we are to show how do we eliminate   -rules and chain rules. This is not the end, as we may still have rules of the form A → α where either |α| ≥ 3 or |α| ≥ 2 and α contains terminals.  But, dealing with such rules is a simple recoding matter, and we 1st focus on the elimination  of  -rules and chain rules. It turns out that -rules should be eliminated 1st.

The 1st step to eliminate   -rules is to compute the set E(G) of erasable (or nullable) nonterminals

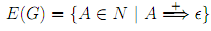
The set E(G) is computed using the sequence of approximations  Ei can be defined as follows:

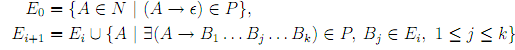
The Ei form an ascending chain

E₀  ⊆ E₁  ⊆ ··· ⊆ E_i ⊆ E_i+1 ⊆ ··· ⊆ N,

and as N  is finite, there is a least i, say i0, such that E_i0 = E_i0+1 . We claim that E(G)= E_i0. 

Email based Automata assignment help - homework help

The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help - Automata homework help and online tutoring with best qualified and experienced computer science tutor's help. We cover all topics including Chomsky Normal Form in assignment help - homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.