Causality in the terms of z-transform, H(z), and the ROC A causal LTI system has an impulse response h(n) = 0 for n < 0, and is, thus, a right-sided sequence. This implies that the ROC of H(z) is the exterior of a circle in z-plane. For the causal system the power series

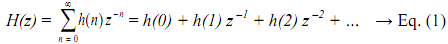
does not have any positive powers of z. As a result, the ROC includes z = ∞ . Thus, we have the principle:

The discrete-time LTI system is causal if the ROC of its system function is exterior of a circle, and includes z =∞.

The initial value theorem states that for the causal sequence, h(n), the initial value can be given by

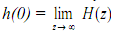
This can be seen by setting z→ ∞ in Eq. (1) making all the terms go to zero except h(0).

Therefore, for a causal sequence, h(n), if h(0) is finite, then, lim H (z) is finite. As a result, with H(z) expressed as the ratio of polynomials in z, the order of the numerator polynomial can't be greater than the order of the denominator polynomial or, consistently, the number of finite zeros of H(z) cannot be greater than the number of finite poles.

The above discussion can summed up as follows: A discrete-time LTI system with the rational system function H(z) is causal if

1.   The ROC is exterior of circle outside the outermost pole, and,

2.   With H(z) as the ratio of polynomials in z, (the positive powers of z), the order of numerator is not greater than the order of denominator.

Condition 1 is not enough alone because the sequence can be right-sided but not causal.

If H(z) can be represented as a ratio of polynomials in z as

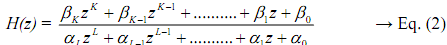
then L ≥ K if the system is causal - or we can say that denominator degree ≥ numerator degree. On the other hand, if we state H(z) as the ratio of polynomials in z ^-1 as

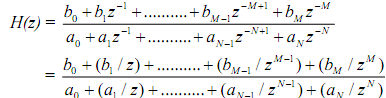
then, if the system is causal, a₀ ≠ 0.  This can be seen by setting z→ ∞ , and requiring that h(0) = (b₀/a₀) be finite. This can be illustrated with the example where a₀ = 0, for example

When H(z) can be written as a ratio of polynomials in z (positive power of z), as in Equation (2), we have required that L ³ K for causality. These L and K are not confused with N and M contained in the difference equation.  Consider, for instance, the system

y(n) + a y(n-1) = x(n) + b x(n-3)

where, in accordance to the notation of the difference equation, N = 1 and M = 3. Apparently M is greater than N and this is permissible. Or we can say that there is no restriction on the relative values of N and M. For, the transfer function can be given by

and it is seen that the numerator degree (K = 3) is not greater than the denominator degree (L =3). Therefore the system is causal.

As another example consider y(n) + a y(n-1) = x(n) + b x(n+1) which is non-causal due to the x(n+1) term. The transfer function can be given by

Note that, when numerator and denominator are expressed in the terms of negative powers of z, "a₀" = 0. Conversely when the numerator and denominator can be expressed in terms of positive powers of z, we have

with the numerator degree greater than denominator degree.

Email based Causality in the terms of z-transform assignment help - Causality in the terms of z-transform homework help at Expertsmind

Are you finding answers for Causality in the terms of z-transform based questions? Ask Causality in the terms of z-transform questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Causality in the terms of z-transform assignment help -Causality in the terms of z-transform homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours