Causality

The constraints of linearity and time-invariance define a class of systems that is represented by the convolution sum. Additional constraints of stability and causality define a more restricted class of linear time-invariant systems of practical importance.

Definition 

The discrete-time system is causal if output at n = n₀ depends only on the input for n ≤ n₀.

The word "causal" has to do with cause and effect; in other words, for the system to act up there must be an actual cause. A causal system doesn't predict future values of the input but only responds to the actual input present. As a result, if the 2 inputs to a causal system are identical up to some point in time n₀ the corresponding outputs should also be equal up to this same time. The synonyms of "causal" are "realizable" and "non-anticipatory".

We digress below to introduce memory-less versus dynamic systems and then resume with causality.

Systems with and without memory A system is said to be static or memory-less if its output for each value of n is dependent only on the input at that same time but not on past or future inputs.

Examples of static systems

1.   y(n) = x(n)       → the identity system

2.   y(n) = a x(n) - x²(n)

3.   A resistor R:    y(t) = R x(t)     (y(t) is voltage and x(t) is current)

In many physical systems, memory is directly associated with storage of energy. A resistor has no storage of energy. However, a circuit with capacitors and/or inductors has storage of energy and is a dynamic system, that is, has memory. However, while storage of energy has to do with only the past inputs, a static system is independent not only of the past but of the future inputs also.

Examples of systems with memory, that is, dynamic systems:

1. 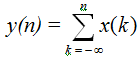 This is an accumulator or summer. The output y(n) depends on values of x(.) prior to n such as x(n-1) etc.

2.   y(n) = x(n-1). This is a delay element.

3.   A capacitor C: 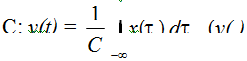 is voltage and x(.) is current).

Getting back to causality, all memory-less systems are causal since the output responds only to the current value of the input. In addition, some dynamic systems (such as the three listed above) are also causal.

An example of a noncausal system is y(n) = x(n) + x(n+1) since the output depends on a future value, x(n+1).

Although causal systems are of great importance, they are not the only systems that are of practical importance. For example, causality is not often an essential constraint in applications in which the independent variable is not time, such as in image processing. Moreover, in processing data that have been recorded previously (non real-time), as often happens with speech, geophysical, or meteorological signals, to name a few, we are by no means constrained to causal processing. As another example, in many applications, including historical stock market analysis and demographic studies, we may be interested in determining a slowly varying trend in data that also contain higher frequency fluctuations about that trend. In this particular case, a commonly used approach is to average data over the interval in order to smooth out fluctuations and keep only the trend. The example of a noncausal averaging system is 

  y(n) = 1/2M+1 ∑x(k)

Definition 

A discrete-time sequence x(n) is called as causal if it has zero values for n < 0, that is, x(n) = 0 for n < 0.

Theorem A linear shift-invariant system with impulse response h(n) is causal if h(n) is zero for n < 0.

Proof of the "If" part By convolution of the output y(n) can be given by

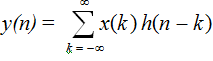
If h(n) = 0 for n < 0, then h(n-k) = 0 for n-k < 0 or k > n. So

Therefore, y(n) at any time n is a weighted sum of the values of the input x(k) for k ≤ n, that is, only the present and past inputs. Hence, the system is causal.

Proof of the "Only If" part 

This is proved by contradiction, that is, if h(n) is non zero for n < 0 then the system is noncausal. Let h(n) be nonzero for n < 0:

h(n) is non zero for n < 0        → h(n-k) is non zero for n-k < 0 or k > n

→ the 2^nd sum above, 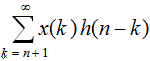, is non zero

→ y(n) then depends on x(n+1) and other future terms

→ Hence, the system is noncausal

Example Check the causality of the system y(n) = x(-n).

Answer If n is some positive value then y(n) depends only on past values of the input x(.). But if n is negative, say n = -2, then

y(-2) = x(-(-2)) = x(2), a future value of input

Hence the system is noncausal.

Email based Causality -Discrete time systems assignment help - Causality -Discrete time systems homework help at Expertsmind

Are you finding answers for Causality -Discrete time systems based questions? Ask Causality -Discrete time systems questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Causality -Discrete time systems assignment help -Causality -Discrete time systems homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours