Cancellation of sampling time in warping and pre-warping The digital specifications are the group of critical frequencies {ω₁, ω₂, ..., ω_N} and the corresponding set of magnitude needs {K₁, K₂, ..., K_N}. When an analog filter is needed as the prototype for the bilinear transformation function the relationship between analog and digital frequencies is nonlinear and proved by

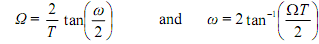
Therefore, to take the proper digital frequency, we have to design an analog filter with analog critical frequencies Ω_i: i = 1, 2, ..., N provided by

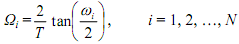
This operation will be defined to as pre-warping. The corresponding analog magnitude needs are not modified and remain the similar as the corresponding digital needs. An analog filter H_a(s) is then designed to satisfy the pre-warped needs shown by Ω₁, Ω₂, ..., Ω_N and K₁, K₂, ..., K_N. The bilinear transformation is then applied to H_a(s), i.e.,

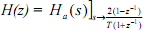
As the T in the Ωi equation and the T in the bilinear transform cancel in the function defined above for low pass filter design, it is convenient to just need T = 1 in both places. This is simply seen since if the Ωi comes from an analog-to-analog transformation of an H_a(s) with a unit radian cut-off frequency, we have s→(s/ Ω_i), and when the bilinear transformation 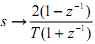 needed the cascade of transformations is provided by 

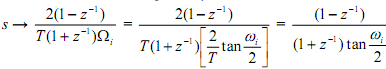
This does not has a T. Thus it is immaterial that value of T is used as long as it is the similar in both steps (which it is).

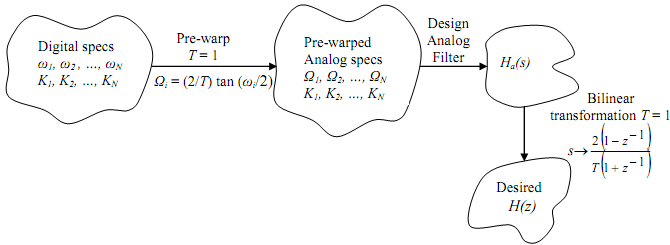
The method for the design of a digital filter needed the bilinear transformation consists of:

Step 1: Pre-warping the digital specifications

Step 2: Designing an analog filter to meet the pre-warped specs

Step 3: Applying the bilinear transformation

In the method T is arbitrarily set to 1, but it may be set simple to any value (e.g., T = 2), since it cancels in the design. The design method is provided by the figure below.

Email based Cancellation of sampling time in warping and pre-warping assignment help - Cancellation of sampling time in warping and pre-warping homework help at Expertsmind

Are you finding answers for Cancellation of sampling time in warping and pre-warping based questions? Ask Cancellation of sampling time in warping and pre-warping questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Cancellation of sampling time in warping and pre-warping assignment help -Cancellation of sampling time in warping and pre-warping homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours