Bounded input bounded output stability

Definition 

A sequence x(n) is bounded if there is a finite M so that |x(n)| < M for all n. (Note that, as expressed here, M is a bound for the negative values of x(.) as well. The other way of writing this is -M < x(n) < M.)

As an example, the sequence x(n) = [1+cos 5Πn] u(n) is bounded with |x(n)| ≤ 2. The sequence 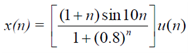 is unbounded.

Definition
A discrete-time system is BIBO which is bounded input-bounded output stable if every bounded input sequence x(n) generates a bounded output sequence. That is, if |x(n)| ≤ M < ∞, then y(n) ≤ L ≤ ∞

BIBO stability theorem 

A linear shift invariant system with the impulse response of h(n) is bounded input-bounded output stable if and only if S, defined which is below, is finite.

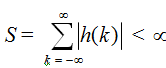
that is, the unit sample response is absolutely summable.

Proof of the "If" part 

The system is given with impulse response h(n), let x(n) be such that |x(n)| £

M. Then output y(n) can be given by the convolution sum:

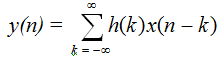
so that

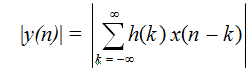
By using the triangular inequality that sum of magnitudes ≥ magnitude of sum, we get

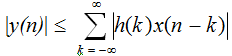
By using the fact that the magnitude of a product is product of the magnitudes,

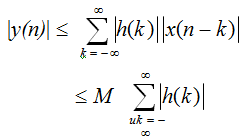
Thus, a sufficient condition for the system to be stable is that the unit sample response should be absolutely summable; that is,

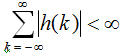
Proof of the "Only If" part
That it is also a necessary condition can be seen by considering as input, the following bounded signal (this is the signum function),

Or, equivalently,

1     where h(k) > 0

x(n-k) = sgn [h(k)] = 0      where h(k) = 0

     -1     where h(k) < 0

In the above we have implied that M = 1 (since M is some arbitrary finite number), and that |x(n)| ≤ 1. If, however, |x(n)|≤ M where M is finite but not equal to 1 we then will multiply the signum function by M. In either case x(n) is a bounded input. Thus

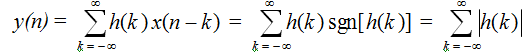
Clearly, if h(n) is not absolutely summable, y(n) will be unbounded. For a causal system the BIBO stability condition becomes

Email based Bounded input bounded output stability assignment help - Bounded input bounded output stability homework help at Expertsmind

Are you finding answers for Bounded input bounded output stability based questions? Ask Bounded input bounded output stability questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Bounded input bounded output stability assignment help -Bounded input bounded output stability homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours