Binomial expression:

An algebraic expression having two terms is known as a binomial expression.

For example, (a + b), (2x - 3y), 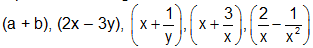 etc. are binomial expressions.

Binomial theorem:

Such equation by which any power of a binomial expression may be expanded in the form of a series is called as Binomial Theorem. For a positive integer n , the expansion is provided by 

(a+x)ⁿ = ⁿC₀aⁿ + ⁿC₁a^n-1 x + ⁿC₂ a^n-2 x²  + . . . +  ⁿC_r a^n-r x^r  + . . . +  ⁿC_nxⁿ = .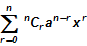

where ⁿC₀ ,  ⁿC₁ ,  ⁿC₂ , . . . , ⁿC_n are known as Binomial co-efficients. Similar as

(a - x)ⁿ = ⁿC₀aⁿ - ⁿC₁a^n-1 x + ⁿC₂ a^n-2 x² - . . . + (-1)^{r n}C_r a^n-r x^r + . . . +(-1)^{n n}C_nxⁿ

i.e. (a - x)ⁿ =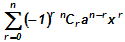 

Replacing a = 1, we obtain

(1 + x)ⁿ = ⁿC₀ +ⁿC₁x+ⁿC₂x² + . . . + ⁿC_r x^r  + . . . + ⁿC_nxⁿ

and (1 - x)ⁿ = ⁿC₀ -ⁿC₁x+ⁿC₂x² - . . . + (-1)^{r n}C_r x^r  + . . . +(-1)^{n n}C_nxⁿ

Observations:

• There  are (n+1) terms in the relation of (a +x)ⁿ.
• Sum of powers of x and a in each and every term in the expansion of (a +x)ⁿ is constant and same to n.
• The basic term in the  expansion of ( a+x)ⁿ is (r+1)^th term provided as T_r+1 = ⁿC_r a^n-r x^r 
• The p^th  term  from  the  end  = ( n -p + 2)^th term from the  beginning .
• Coefficient of x^r in expansion of  (a + x)ⁿ  is ⁿC_r a^{n - r} x^r.
• ⁿC_x = ⁿC_y Þ x = y or x + y = n.
• In the expansion of (a + x)ⁿ and (a -x)ⁿ, x^r occurs in (r + 1)^th term. 

Email based Binomial theorem Assignment Help -Binomial theorem Homework Help

We at www.expertsmind.com offer email based Binomial theorem assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.

Expertsmind's best education services

• Quality assignment-homework help assistance 24x7 hrs
• Best qualified tutor's network
• Time on delivery
• Quality assurance before delivery
• 100% originality and fresh work