Bilinear transformation:

One method to the numerical solution of an ordinary linear constant-coefficient differential equation is laid on the application of the trapezoidal principle to the first order approximation of integration. Consider the given equivalent pair of equations

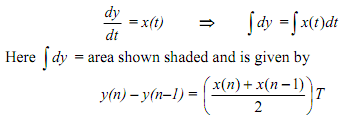
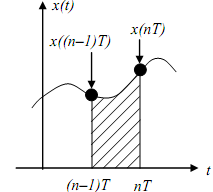
where we have used the trapezoidal rule to calculate the area under a curve.

Taking the z transform of the above we get

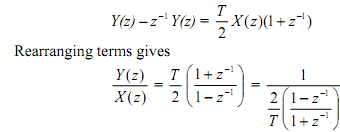
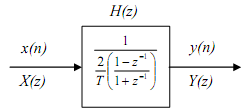
Thus the continuous time system y(t) = ∫x(t)dt shown by the following block diagrams

is replaced in the discrete-time domain by the given block.

In other words, given the Laplace transfer function Ha(s), the corresponding digital filter is given by replacing s with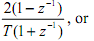

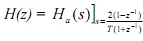
This is known as bilinear transformation (both numerator and denominator are first order polynomials), also called as bilinear z-transformation (BZT).

Here again, note that at that point we have not given how Ha(s) was calculated, but rather we are define how to calculate the digital filter H(z) from any given Ha(s) taking bilinear transformation.

Email based Bilinear transformation assignment help - Bilinear transformation homework help at Expertsmind

Are you finding answers for Bilinear transformation based questions? Ask Bilinear transformation questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Bilinear transformation assignment help -Bilinear transformation homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours