It states that the total energy (pressure energy, potential energy and kinetic energy) of an incompressible and non-viscous fluid in steady flow through a pipe remains constant throughout the flow, provided there is no source or sink of the fluid along the length of the pipe.
This statement is related on the consideration that there is no loss of power due to friction.
Mathematically, for unit volume of fluid going through a pipe.
P/ρ + gh + 1/2 v2= constant ..... (i)
Proof. To prove Bernoulli's theorem, we have the given assumptions:
1. The liquid is incompressible.
2. The liquid is non-viscous.
3. The flow is steady and the velocity of the liquid is less than the critical velocity for the liquid.
|
Imagine an incompressible and non-visous liquid to be flowing through a pipe of varying cross-sectional area as given in diagram. The liquid goes into the pipe with a normal velocity v1 at its wide end A of cross-sectional area a1 and at a height h1 above the reference level (earth's surface). It replaces the pipe with an actual speed v2 at the narrow end B of cross-sectional area a2 and at a height h2 above the earth's surface.
|
|
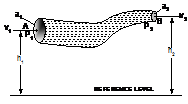
If r is the density of the incompressible liquid, then in according with the relation of continuity, the mass m of the liquid crossing any part of the pipe is shown by
a1 v1 r = a2 v2 ρ = m (say) or a1 v1 = a2 v2 = m/ρ ..... (ii)
Let P1 and P2 be the values of the pressure due to the liquid at the ends A and B respectively. If the liquid goes from the end A to B under the action of pressure difference P1 - P2, then in accordance with energy conservation rule, the work done by the pressure power of the liquid have to be appeared as the increase in potential and kinetic energies of the liquid.
The pressure energy operated a force P1 a1 on the liquid at last point A. The liquid goes a distance v1 in one second at the end A and therefore
Work completed per second on the liquid at the end A = ρ1 a1 v1
The liquid goes the end B against pressure P2 i.e. against a friction force P2 a2. At the end B, the liquid goes a distance v2 in one second and therefore
Work completed per second by the liquid at the end B = r2 a2 v2
Hence, total work done by the pressure energy in going the liquid from the end A to B in one second = r1 a1 v1 - r2 a2 v2
Using the equation (ii), we have
Net work done by the pressure energy per second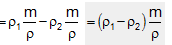 
... (iii)
When the volume m of the liquid flows in one second from the end A to B, its height increases from h1 to h2.
Therefore, increase in potential energy of the liquid per second
= m g h2 - m g h1 = m g (h2 - h1) ... (iv)
Further, when the volume m of the liquid goes in one second from the end A to B, its velocity increases from v1 to v2.
Therefore, increase in kinetic energy of the liquid per second =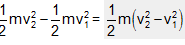 
... (v)
According to work-energy conservation principle,
Work completed by the pressure power per second = increase in potential energy per second + increase in kinetic energy per second
or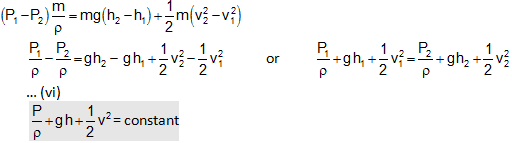 
It proves the Bernoulli's theorem. This is the biggest convenient type of Bernoulli's relation. However, it may be denoted in some other forms as explained below:
Multiplying both sides of the equation (vi) by r, we have
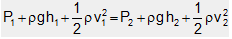... (vii)
In this relation, each part has got dimension of pressure.
Again, dividing both sides of the equation (vi) by g, we have
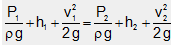.... (viii)
In this equation, each term has got dimensions of length. The terms P/ρg, h and v2/2g are called pressure head, velocity head and elevation head and respectively.
When the liquid flows through a horizontal pipe (h1 = h2), then the equation (vi) becomes
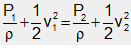
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Bernoulli’s theorem questions? Bernoulli’s theorem topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Bernoulli’s theorem related problems. We provide step by step Bernoulli’s theorem question's answers with 100% plagiarism free content. We prepare quality content and notes for Bernoulli’s theorem topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours