Asymptote of hyperbola:

The straight line, to which the tangent to the curve tends as point of contact tends to approach infinity, is called as asymptote of the curve. Or we can say that asymptotes tend to touch the curve at infinity.

   Asymptote of  curve may be  defined in another  way A straight  line which touches the given curve at infinity but the line itself is not at infinity is called an asymptote to given curve.

Equation of the asymptotes:

Let y = mx + c be an asymptote of hyperbola 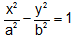   .....(i)

Substituting value of y in (1),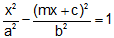 

or         (a²m² - b²) x² + 2a²mcx + a²(b² + c²) = 0                    .....(ii)

If line y = mx + c is an asymptote to the given hyperbola, then it touches hyperbola at infinity. So both the roots of (2) should be infinite.

∴a²m² - b² = 0 & -2a² mc = 0 then m = ± b/a & c = 0

substituting value of m & c in y = mx + c, we get

y = ± b/a.Hence equation of asymptotes is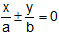 

Alternative Method:

Let the equation of hyperbola be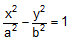 

The tangent at P(x₁, y₁) on it is 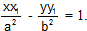= 1. But (x₁, y₁) lies on hyperbola

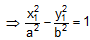
By eliminating y₁ from above equations, we find that equations of 2 tangents to the curve at the point with the abscissa x₁ are

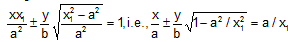
Taking limits when x₁ tends to infinity, we have equations of asymptotes as x/a + y/b = 0.

Note: 

(i) There are 2 asymptotes both passing through centre and equal inclined to axis of x the inclination being tan^-1 (b/a).

(ii) The angle between 2 asymptotes is 2 tan^-1 (b/a).

(iii) The difference between the 2^nd degree curve and pair of asymptotes is constant.

(iv) A hyperbola and its conjugate hyperbola have same asymptotes.

(v)  The equation of hyperbola and that of its pair of asymptotes differ by constant. For instance, if S = 0 is equation of the hyperbola, then combined equation of asymptotes can be given by S + K = 0. The constant K can be obtained from condition that the equation S + K = 0 represents a pair of lines. Finally  the  equation of  the   corresponding  conjugate hyperbola  is  S+ 2K = 0.

(vi) If b = a then 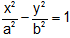 reduces to x² - y² = a². The asymptotes of rectangular hyperbola x² - y² = a² are y = ±x which are at the right angles.

Email based Asymptote of hyperbola Assignment Help -Asymptote of hyperbola Homework Help

We at www.expertsmind.com offer email based Asymptote of hyperbola assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.

Expertsmind's best education services

• Quality assignment-homework help assistance 24x7 hrs
• Best qualified tutor's network
• Time on delivery
• Quality assurance before delivery
• 100% originality and fresh work