Application of linearity - Convolution

An arbitrary sequence, x(n), can be written as the weighted sum of delayed unit sample functions:

x(n) = ...+ x(-2) δ(n+2) + x(-1) δ(n+1) + x(0) δ(n) + x(1) δ(n-1) +...

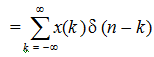
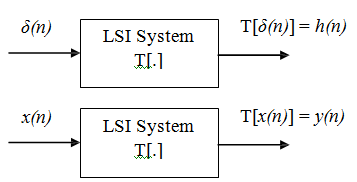
So the response of a linear system to input x(n) can be written down using the linearity principle, that is, linear superposition. For a linear shift-invariant system the impulse response of which is T[δ(n)] = h(n) the reasoning goes like this

• For the input δ(n) output is h(n). For the input x(0) δ(n) the output is x(0) h(n) by the virtue of scaling.

• For the input δ(n-1) the output is h(n-1) by virtue of shift invariance. For an input x(1) δ(n-1) the output is x(1) h(n-1) by virtue of scaling.

• Thus for the input of x(0) δ(n) + x(1) δ(n-1) output is x(0) h(n) + x(1) h(n- 1) by virtue of the additivity property.

This reasoning is extended to cover all the terms which make up x(n). Generally the response to x(k) δ(n-k) can be given by x(k) h(n-k).

Given that

h(n) = T[δ(n)],  and x(n) =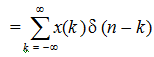 

we have

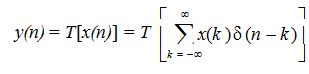
As T[.] is linear we can apply linearity of the countable infinite number of times to write

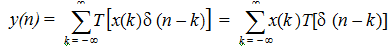
In the equation stated above since the system is shift-invariant we write T[δ(n-k)] = h(n-k). Otherwise write hk(n) or h(n, k) in place of h(n-k). Therefore for a linear shift-invariant system

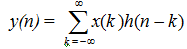
Note that if the system is not specified to be shift-invariant we would leave the above result in the form

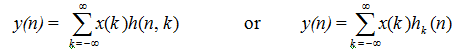
Then if the shift-invariance is invoked we replace h(n, k) with h(n-k).

As in the case of continuous-time systems, impulse response, h(n), can be determined considering that the system has no initial energy; else the linearity property does not hold, so that y(n), as determined using the above equation, corresponds to the forced response of the system only.

The sum x(k )h(n, k ) is called as convolution sum, and is denoted x(n) * h(n).

A discrete-time linear shift-invariant system is characterized by its unit sample response h(n).

Email based Application of linearity – Convolution assignment help - Application of linearity – Convolution homework help at Expertsmind

Are you finding answers for Application of linearity – Convolution based questions? Ask Application of linearity – Convolution questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Application of linearity – Convolution assignment help -Application of linearity – Convolution homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours