|
Angular displacement:
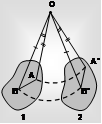
Take a rigid body undergoing rotation related to an axis, perpendicular to the plane of the paper and passing through O. Consider that A and B are any two particles of the rigid body at the position 1 while A¢ and B¢ are their subsequent locations when the body is at the position 2.
Since the body undergoes rotation,
OA = OA′ and OB = OB′
Further AB = A′B′, since the body is rigid.
 ΔOAB ≡ ΔOA′B′(congruent) ΔOAB ≡ ΔOA′B′(congruent)
|
|
i.e. ∠AOB = ∠A′OB′
Adding ∠AOB′ to both sides of the above relation, we get
∠BOB′ = ∠AOA′ = θ (say)
This shows that in a given interval of time the angular displacements of all particles of the rigid objects undergoing rotation are identical.
Therefore, a single variable, viz. angular displacement (θ) may be used to define the rotational motion of the rigid object.
Angular velocity:
The power of change of angular displacement with respect to time is called as angular velocity.
Average angular velocity: The power of change of angular displacement with related to time is called as angular velocity.
To describe average angular velocity it is necessary to specify the interval in which we are talking for average. 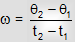
Instantaneous angular velocity: Concurrent velocity seems angular velocity at a particular instant. It is mathematically shown as ,
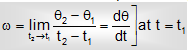
Angular accelerations (ω):
The rate of change of angular velocity with related to time is called as angular acceleration.
Average angular acceleration: It is important to denote the time interval to in which we are talking about average.
In a given time interval t1 to t2 the average angular acceleration is described as,
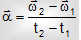
Instantaneous angular acceleration: Concurrent angular acceleration means angular acceleration at a particular dot instant at t = t1 mathematically it is shown as,
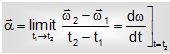
Direction of angular acceleration: If value of ω increasing then direction of a will be equal as direction of ω and vice-versa.
Equation of angular motion:
ω(t) = ωo + at
θ(t) = θo + ωot + 1/2αt2
ω2(t) = ω02 +2αθ
Here ωo = magnitude of the initial angular velocity
ω(t) = value of the angular velocity after time t.
θo = Initial angular position.
θ(t) = Angular position after time t.
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Angular displacement,Velocity and Accelerations questions? Angular displacement,Velocity and Accelerations topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Angular displacement,Velocity and Accelerations related problems. We provide step by step Angular displacement,Velocity and Accelerations question's answers with 100% plagiarism free content. We prepare quality content and notes for Angular displacement,Velocity and Accelerations topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours