Analytical method of finding the resultant of two simple harmonic motions in the same direction when they have the same periodic time.
The two S.H.Ms having the same periodic time can be represented by the equations
y1 = a1 sin(ωt - δ1) or y2 = a2 sin(ωt - δ2)
Since the displacement y1 and y2 are in the same point, the resultant distance y at any time t is obtained by their algebraic addition, or
|
y = y1 + y2
= a1 sin(ωt - δ1) + a2 sin(ωt - δ2)
= a1sinωt cosδ1- a1cosωt sinδ1) + a2sinωt cosδ2- a2cosωt sinδ2)
= sinωt(a1cosδ1+ a2cos δ2) - a2 cosωt (a1sinδ1 + a2sinδ2)
Now take an angle f as shown in figure such that a
acosΦ = a1cos δ1 + a2cosδ2 and a sinΦ = a1sinδ1+ a2sin δ2
Then, y = asinωt cosΦ - a cosωt sinΦ
= asin(ωt - Φ),
|
|
This represents a simple harmonic motion of the same periodic time as the component motions and having an amplitude = a and epoch angle = f. From figure a is given by the relation
a2 = (a1sinδ1+ a2sin δ2)2 + (a1cos δ1 + a2cosδ2)2
= (sin2δ1+ cos2δ1) + (sin2 δ2+ cos2δ2) + 2a1a2(sinδ1 sinδ2+ cosδ1cosδ2)
= cos(δ1 - δ2) And f is given by the relation
The results are the same as those obtained graphically in the previous article.
Proceeding in a similar manner as given, it can be given that, for a number of simple harmonic motions acting on a point in the same direction when their periodic times are same, amplitude of the resultant speed is shown by,
,
The epoch of the resultant is shown by, 
In case of superposition of two SHM's:
(a) In the similar direction and of same frequency.
If Θ=0, both SHM's are in phase and A=A1+A2
If Θ= ∏, both SHM's are out of phase and 
The resultant value due to superposition of two or more than two SHM's of this case can also be found by phases diagram also.
(b) In same direction but are of different parts.
then resultant displacement 
(c) In two perpendicular directions
Case (i) if so path will be straight line & resultant displacement will be 
Case (ii) if
So, resultant will be .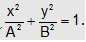
i.e. equation of an ellipse and if A = B, then the resultant will be circle.
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Analytical method of simple harmonic motion questions? Analytical method of simple harmonic motion topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Analytical method of simple harmonic motion related problems. We provide step by step Analytical method of simple harmonic motion question's answers with 100% plagiarism free content. We prepare quality content and notes for Analytical method of simple harmonic motion topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours