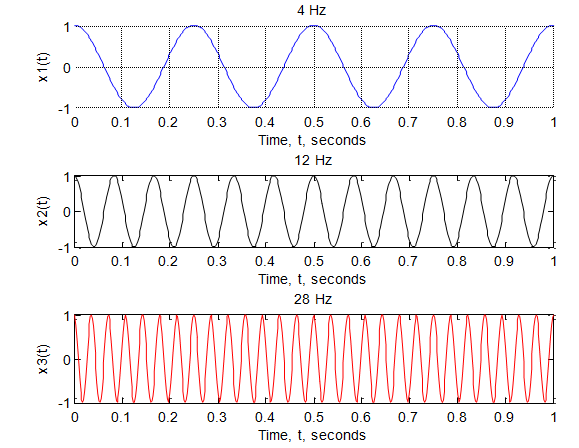
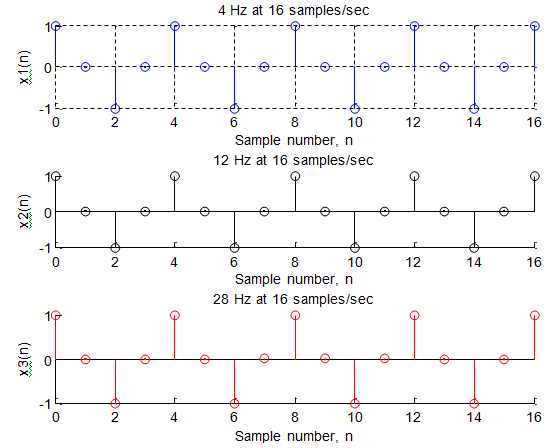
Aliasing and digital frequency With F_s = 16 Hz the base band signal should be band-limited to 8 Hz. And we don't expect frequencies higher than 8 Hz. Consider the 3 signals x₁(t), x₂(t), and x₃(t) of frequencies 4Hz, 12Hz and 28Hz, respectively, here x₂ and x₃?s frequencies are the aliases of x₁?s. The continuous and discrete-time signals are given in the table below with the sampling rate of 16 samples/sec.

If Nyquist criterion is to be satisfied (for the perfect signal reconstruction) we do not expect digital frequencies higher than 0.5 cycle/sample (or π rad./sample) in base band signal. This corresponds to taking two samples for every cycle (or digital frequency of half a cycle per sample) - the Nyquist criterion. The Digital frequencies higher than 0.5 cycle (x2(n)and x3(n) in this example) are actually not allowed.

When plotted x₁(n), x₂(n), and x₃(n) can't be distinguished from one another for

the digital frequency. They all have a period = 4 and a frequency of 0.25 cycle per sample, and we know that x₂(n) has a frequency of 0.75 cycle and x₃(n) has a frequency of 1.75 cycle.

Generally any digital frequency above 0.5 cycle (π rad./sample) is an alias (or shows up as an alias of some base band frequency). It in fact has more cycles per sample than is apparent in a plot of sampled data.

The phenomenon of aliasing using the 2 waveforms x₁(t), x₂(t), and x₃(t) and the corresponding sequences x₁(n), x₂(n), and x₃(n) is demonstrated below.

In MATLAB:

%Aliasing demo

%First---------------------------------------------

%Plot the continuous-time waveforms x1(t), x2(t), and x3(t) over a 1-second interval t = 0: 1/500: 1;

x1 = cos (2*pi*4*t); %4 Hz

subplot(3, 1, 1), plot(t, x1, 'b');           %subplot(3, 1, 1) - 3 rows, 1 column, #1 xlabel ('Time, t, seconds'), ylabel('x1(t)');

title ('4 Hz')

grid;

x2 = cos (2*pi*12*t); %12 Hz

subplot(3, 1, 2), plot(t, x2, 'k');           %subplot(3, 1, 2) - 3 rows, 1 column, #2 xlabel ('Time, t, seconds'), ylabel('x2(t)');

title ('12 Hz')

x3 = cos (2*pi*28*t); %28 Hz

subplot(3, 1, 3), plot(t, x3, 'r');            %subplot(3, 1, 3) - 3 rows, 1 column, #3 xlabel ('Time, t, seconds'), ylabel('x3(t)');

title ('28 Hz')

%Second---------------------------------------------

%Plot the sequences x1(n), x2(n), and x3(n)

n = 0: 1: 16;

%4 Hz sampled at 16 Hz x1 = cos (n*pi/2);

subplot(3, 1, 1), stem(n, x1, 'bo');       %subplot(3, 1, 1) - 3 rows, 1 column, #1 xlabel ('Sample number, n'), ylabel('x1(n)');

title ('4 Hz at 16 samples/sec')

grid;

%12 Hz sampled at 16 Hz x2 = cos (3*n*pi/2);

subplot(3, 1, 2), stem(n, x2, 'ko');       %subplot(3, 1, 2) - 3 rows, 1 column, #2 xlabel ('Sample number, n'), ylabel('x2(n)');

title ('12 Hz at 16 samples/sec')

%28 Hz sampled at 16 Hz x3 = cos (7*n*pi/2);

subplot(3, 1, 3), stem(n, x3, 'ro');        %subplot(3, 1, 3) - 3 rows, 1 column, #3 xlabel ('Sample number, n'), ylabel('x3(n)');

title ('28 Hz at 16 samples/sec')

%---------------------------------------------

Email based Aliasing and digital frequency assignment help - Aliasing and digital frequency homework help at Expertsmind

Are you finding answers for Aliasing and digital frequency based questions? Ask Aliasing and digital frequency questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Aliasing and digital frequency assignment help -Aliasing and digital frequency homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours