Algebra of matrices:

Addition and Subtraction of Matrices:

Any two matrices may be included if they are of the similar order and the resulting matrix is of the similar order.  If two matrices A and B are of the exact order, they know as conformable for addition.

For example: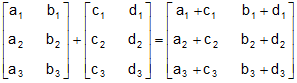             

Similarly,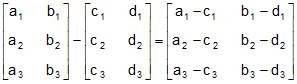 

Notes:                       

• Only matrices of the similar order may be subtracted or added.

Scalar Multiplication:

The matrix calculated by multiplying each and every element of a matrix A by a scalar l is known as the scalar multiple of A by l .

For example: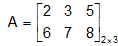                                  

Therefor,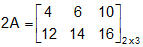 

Properties:   

All the rules of general algebra hold for the subtraction or addition of matrices and their multiplication by scalars.

(i).           If A and B be two matrices of the similar order and if k be a scalar, then

                k(A + B) = kA + kB

(ii).          If k₁ and k₂ are two scalars and if A is a matrix, then

                (k₁ + k₂)A = k₁A + k₂A and k₁(k₂A) = k₂(k₁A)

Multiplication of Matrices:

Two matrices may be multiplied only when the number of columns in the first is same to the number of rows in the second.  Such matrices are called conformable for multiplication.

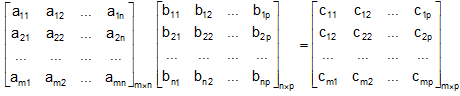
where c_ij = a_i1 b_1j + a_i2 b_2j + .......+ a_in b_nj =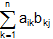 

Example: 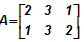    and 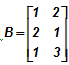, show that AB ≠ BA.

Solution:       

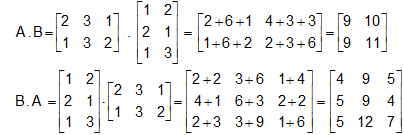
                        Thus A .B  ≠ B . A.

Notes:           

• Commutative law does not essentially hold for matrices.
• Matrix multiplication always associative.
• Matrix multiplication always distributive with respect to addition.
• If A is a square matrix of order n and if I_n is an identity matrix of order n, then AI_n=I_nA=A.
• If I be a unit matrix, then I = I² = I³ = ...... = Iⁿ.

Email based Algebra of matrices Assignment Help -Algebra of matrices Homework Help

We at www.expertsmind.com offer email based Algebra of matrices assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.

Expertsmind's best education services

• Quality assignment-homework help assistance 24x7 hrs
• Best qualified tutor's network
• Time on delivery
• Quality assurance before delivery
• 100% originality and fresh work