Adjoint of a Square Matrix:

Suppose A = [a_ij] be a square matrix of order n and let C_ij be cofactor of a_­ij in A. Then the transpose of the given matrix of cofactors of components of A is known as the adjoint of A and is shown by adj A.

Therefore, adjA = [C_ij]^T  Þ (adj A)_ij = C_ji

If A = , then, adjA = ;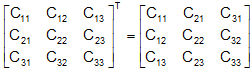

where C_ij shows the cofactor of a_ij in A.

For Example:  A = 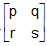, C₁₁ = s, C₁₂ = -r, C₂₁ = -q, C₂₂ = p

∴ adj A = .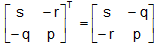

Theorem: Suppose A be square matrix of n^th order. Then A(adj A) = |A| I_n = (adj A)A

Inverse of a Matrix:

A non-singular square matrix of n^th order is invertible if there exists a square matrix B of the similar order such that  AB = I_n = BA.

In that a case, we can say that the inverse of A is B and we can write, A^-1 = B.

The inverse of A is provided by A^-1 = 1/|A|. adj A

Properties of Inverse of a Matrix:

 (i). (Reversal Law) If A and B are invertible matrices of the similar order, then AB is invertible and (AB)^-1 = B^-1A^-1. usual, if A, B, C, .... are invertible matrices then

            (ABC.....)^-1 = .....C^-1B^-1A^-1

(ii). The inverse of the inverse of the matrix is the original matrix itself, i.e. (A^-1)^-1 = A. 

Email based Adjoint and Inverse of a Matrix Assignment Help -Adjoint and Inverse of a Matrix Homework Help

We at www.expertsmind.com offer email based Adjoint and Inverse of a Matrix assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.

Expertsmind's best education services

• Quality assignment-homework help assistance 24x7 hrs
• Best qualified tutor's network
• Time on delivery
• Quality assurance before delivery
• 100% originality and fresh work