A Circular Queue

         A circular queue is one in which the insertion of a new element is done at the very first location of the queue if the last location of the queue is full. In other words if we have a queue Q of say n elements then after inserting an element last (i.e. in the n_1th) location of the array the next element will be inserted at the very first location (i.e. location with subscript 0) of the array it is possible to insert new elements if and only if those location (slots) are empty. We can say that a circular queue is one in which the first elements comes just after the last element it can be viewed as a mesh or loop of wire in which the two ends of the wire are connected together fig 6.5 shows a empty circular queue Q[5] which can a accommodate five elements.

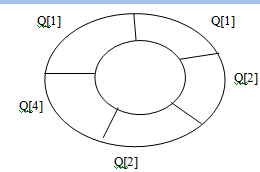
Insertion: consider the circular queue shown above the insertion in this queue will be same as with linear queue, we only have to keep track of Front and Rear with some extra logic. A Circular Queue is shown in the figure 6.6.a.

   If more elements are added to the queue, it looks like shown in figure 6.6.b.

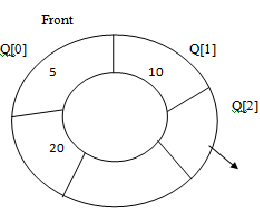
Now the queue will be full. If we now try to add another element to the queue, as the new elements is inserted from the Rear end, the position of the element to be inserted will be calculated by the relation:

                           Rear = (Rear + 1) % MAXSIZE

For the current queue (Fig.6.6.b.) the value of Rear is 4 and value of MAXSIZE is 5 hence

                           Rear = (Rear + 1) % MAXSIZE

                           Rear = (4+1) % 5      

                                      = 0

 Note that Front is also pointing to Q[0] (Front =0) and Rear also comes out to be 0 (i.e., Rear is also pointing to Q[0]. Since Rear = Front the Queue Overflow condition is satisfied and our trial to add new element will flash the message "Queue Overflow" which avoids us to add new element.

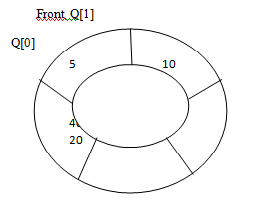
                           Referring to the figure Fig 6.6(c). Consider the situation when we add an element to the queue. The Rear is calculated as follows:

                           Rear = (Rear +1) % 5

                           Rear = (5+1) % 5

                                   = 0.

The new element will be added to Q[Rear] or Q[0] location of the array and Rear is incremented by one (i.e. Rear = 1= 0+1) The next element will be added to location Q[1] of the array.

Deletion. The deletion method for a circular queue also requires some modification as compared to linear queues.

In the above figure Fig 6.7 the queue is full. Now if we delete one element from the queue. It will be deleted from the Front end. After deleting the front element the front should be modified according to position of Front. That is if Front indicates to the last element of the circular queue the after deleting heat element the Front should be again reset to 0 (Front = 0) otherwise after every deletion the new position which Front should indicate will be given as:     

                                  Front = (front +1) % MAXSIZE

For example.

Algorithms for addition and deletion in a circular queue (using Arrays)

Data Structure & Algorithms Assignment Help, Live Experts 

Struggling with data structure problems? Data structure subject is quite tough to learn? Need quick assistance in data structure questions? ExpertsMind.com is right place for you where your search ends, We at ExpertsMind offer online data structure assignment help, data structure homework help and data structure and algorithms question's answers by best online support by qualified tutors.

ExpertsMind.com - A Circular Queue Assignment Help, A Circular Queue Homework Help, A Circular Queue Assignment Tutors, A Circular Queue Solutions, A Circular Queue Answers, Queues Assignment Tutors