Introduction: In Co-ordinate Geometry, we study geometry by the methods of algebra. It is ·done by means of a pair of real numbers, associated with every point in a plane called the coordinates. One type of co-ordinates are known as Cartesian co-ordinates.
Axis: Consider any straight line take any point O on it. It divides the line into two parts. One part extends from to its right and the other to its left. One of these two directions is regarded as positive and the other opposite to it is negative. A straight line to which a positive direction is assigned is called an Axis. Positive direction is indicated by the arrowhead. Conventionally, the direction from left to right is taken as positive.
Co-ordinate axes: Let X'OX and Y'OY be two mutually perpendicular lines taken as axis whose positive directions are shown by arrow on the axes. These lines are called the co-ordinate axis.
X'OX is called the x-axis.
Y'OY is called the y-axis.

As the axis taken are mutually at right angles, they are called the Rectangular Axis. If the axis are not mutually at right angles, they are called the Oblique Axis.
The point O (i.e., the point of intersection of the axis) is called the Origin.
Note: In naming the co-ordinates of a point, the x-co-ordinate is written first and then the y-co-ordinate, separated by coma and written within paranthesis ( ).
Caution: Abscissa x is measured in the sense LP and not PL. Ordinate y is measured in the sense MP and not PM.
Sign of Co-ordinates:
(i) Abscissa is taken positive if LP is measured in the same sense as the positive direction of the x-axis i.e., OX and measured negative if direction of LP (not PL) is not of OX'.
(ii) Ordinate is taken positive if MP (not PM) is measured in the same sense as the positive direction of the y-axis i.e., OY and is taken negative if sense of MP is that of OY'.
(a) x-co-ordinate or abscissa of all the points on the y-axis is zero. Thus, any point on the y-axis is of the form (0, y).
(b) y-co-ordinate or ordinate of all the points on the x-axis is zero. Thus, any point-on the x-axis is of the form (x, 0).
(c) Co-ordinates of origin are (0, 0) as it lies on both the axes.

Cor. 1. Distance of the point (x, y,) from origin is given by

Cor. 2. If PL and OM are perpendiculars from P and Q upon X'OX then, LM is called Projection of PO upon x-axis. Thus projection of PQ upon x-axis
= LM = OM - OL = x2 - x1.
Similarly projection of PQ upon y-axis = y2 -y1.
Note:
In questions relating to geometrical figures, take the given vertices in the given order and proceed as indicated.
(i) For an isosceles triangle: At least two sides are equal.
(ii) For an equilateral triangle: Three sides are equal.
(iii) For a right-angled triangle: The sum of the sqaures of two sides is equal to the square of the third side.
(iv) For collinear points: The sum of the distances between two point pairs is equal to the distance between the third point pair.
(v) For a square: The four sides are equal, two diagonals are equal.
Plotting of points: We will plot a point whose co-ordinates (h, k) are given. It is plotted as follows:
(i) Measure OM equal to h along the x-axis.
(ii) Measure MP perpendicular to OM and equal to k.
Also observe the rule of signs in both the cases then P is the required point.
Graph: The graph of an equation in x and y is the locus of all point (x, y) satisfied by the given equation.
Graph, some important points: Each point in a plane is represented by an ordered pair (x, y), x is called the x-coordinate or abscissa and y is called the y-coordinate or ordinate of the point.
The abscissa of a point is the distance of point from y-axis.
The ordinate of a point is the distance of point from x-axis.

Method to draw a graph of any linear equation in two variables :
1. Write the given equation in the form (y = mx + c) i.e., showing one variable in terms of the other.
2. Draw the rectangular axes and choose a suitable scale.
3. Plot three points obtained in step 1.
4. Draw the straight line joining any two of these points and check it with the third point.
It is not necessary that two equations will always have a unique solution. Graphically there can be three possibilities.
Graphical solution of a system of equations:
(1) Line may intersect, they may have only one point in common and then the equation will have a unique solution. Such equations are said to be consistent.
(2) May be coincident, they may have an infinite number of points in common there will be an infinite number of solutions and so consistent.
(3) May be parallel, they may have no point in common. In this case there will be no solution at all. Such equations are said to be inconsistent.
The co-ordinate axes X'OX and YOY' divide the plane of the paper into four equal regions, called quadrants known as 1st, 2nd, 3rd and 4th quadrant.
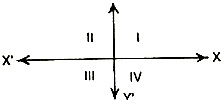
Co-ordinates of the point in 1st, 2nd, 3rd and 4th quadrant have their signs as (+, +), (-, +) (-, -) and (+, -) respectively.
Distance formula: Distance between the points (x1, y1) and (x2, y2)

Cor. 1. Distance of the point (x1, y1) from origin is given by

Area of triangle: The area of a triangle whose vertices are (x1, y1).


Note: The points A, B, C will be collinear if the area of DABC = 0.
Section formula: The points which divides the join of two given points (x1 y1) and (x2, y2) in the ratio m : n are.
 '+' sin considered for internal division while '-' that for external.
'+' sin considered for internal division while '-' that for external.
Note:
(i) a line ax + by + c = 0 divides the join of (x1, y1) and x2, y2) in the ratio

(ii) x-axis divides the join of (x1 y1) and (x2, y2) in the ratio 
(iii) y-axis divides the join of  and (x2, y2) in the ratio
and (x2, y2) in the ratio 
Middle point of the line joining the points (x1, y1) and (x2, y2) is(x1+x2/2,y1+y2/2)
Median of a triangle: It is a straight line joining the vertex of a triangle to the mid-point of the opposite side. Medians are concurrent.
Centroid of a triangle: The centroid of a triangle is the point of intersection of its medians (the line joining a vertex to be middle point of the opposite side). The centroid divides the medians in the ratio
2:1.
If the vertices of a triangle be (x1, y1), (x2, y2) and (x3, y3), then the centroid of the triangle is (x1+x2+x3/3,y1+y2+y3/3)
Circumcentre of a triangle: The point of intersection of the perpendicular bisectors of the sides of a triangle is called its circumcentre.
In centre of a triangle: The centre of the circle which touches the sides of a triangle is called its in centre. It is the point of intersection of the internal bisectors of the angles of the triangle.
If the vertices of the triangle ABC be (x1, y1), (x2, y2) and (x, y3) and the lengths of the sides be a, b, c, then the incentre of the triangle ABC will be

Internal bisectors of the angles of D are concurrent.
Note: Centroid, circumcentre, incentre and ortho centre of an equilateral triangle are same.
Straight line: A line is determined by two points. A relation between x and y satisfied by all the points lying on a straight line and y on other point, is called the equation of that straight line.
SLOPE OF A LINE
The slope (or gradient) of a line is the tangent of the angle which is the part of the line above the x-axis makes with the positive direction of the x-axis (the angle measured is positive i.e., in counterclockwise).
Note: The slope of the line is independent of the sense of the line.

Consider sense AB, then slope = tan q, and consider sense BA, the slope = tan (p + q) = tan q.
\ The slope is the same for both sense of the line.
Slope of the line joining the points (x1, y1) and (x2, Y2) will be

If the slopes of two lines be m1 and m2, then the lines will be
(i) Parallel if m1 = m2
(ii) Perpendicular if m1, m2 = - 1.
Collinearlty of three given points: The three given points A, B, C are collinear e., lie on the same straight line, if
(i) Area of DABC is zero (Area of triangle method)
(ii) Slope of AB = slope of AC
or
(iii) Anyone of the three points (say C) lie on the straight line joining the other two points (Points A and B).
Locus of a point: The locus of a moving point is the path traced out by it under some given geometrical condition or conditions. Plural of Locus is Loci.
Important points: To find the locus of a point, proceed as follows:
Let (h1 k) be the coordinates of the moving point say P. Now using given geometrical conditions find the relations between h, k and other known and unknown quantities. From these relations eliminate the unknown quantities to get a relation between h, k and the known quantities. Now ·the locus of P (h, k) is obtained by generalising (h, k), i.e., by putting x for hand y for k.
Remember that:
(i) If A and Bare two fixed points, then the locus of the point P which moves in such a way that PA + PB = constant, is ellipse.
(ii) As above, if PA - PB = constant, then locus is hyperbola.
(iii) And if PN + PB2 = constant, then locus is circle.
Properties of some geometrical figures:
1. In a triangle ABC, if AD is the median drawn to BC, then AB2 + AC2 = 2(AD2 + BD2).
2. A triangle is isosceles if any two of its medians are equal or two sides are equal.
3. In a right angled triangle, the midpoint of the hypotenuse is equidistant from the vertices.
4. Equilaterial triangles - All sides are equal. Vertices of an equilateral triangle can not be all integral.
5. Rhombus - All sides equal and no angle a right angle, but diagonals are at right angles and unequal.
6. Square - All sides equal and each angle is right angle. The diagonals are also equal.
7. Parallelogram - Opposite sides equal, diagonals bisect each other.
8. Rectangle - Opposite sides equal and each angle a right angle. Diagonals are equal.
9. The figure obtained by joining the middle points of a quadrilateral in order is a parallelogram.
Polar formulae: (1) If (x, y) be cartesian co-ordinates and (r, q) be the polar coordinates of a point, then
x = r cos q, y = r sin q, r =  and q = tan-1 y/x
and q = tan-1 y/x
(2) Distance between two points P(r1 q1) and a (r2, q2) in polar coordinates is given by

(3) Area of triangle in polar coordinates is

Transformation:
(i) Equations of transformation, when origin is shifted to (h, k) axes remaining parallel are x = x1 + h, y = y, + k.
(2) Equations of transformation when origin is fixed and axes are rotated by an angle q are x = x, cos q - y1, sin q and y = x1 sin q + y1 cos q + k.
(3) The general equations of transformation are x = x1 cos q - y1 sin q + h and y = x sin q + y cos q + k.
(4) To remove the term of xy in the equation ax2 + 2hxy + by2 = 0, the angle e through which the axes must be turned (rotated) is given by q
tan-1y/x
Live Math Experts: Help with Rectangular Cartesian Assignments - Homework
Expertsmind.com offers help with Rectangular Cartesian assignment and homework in mathematics subject. Experts mind'smath experts are highly qualified and experienced and they can solve your complex Rectangular Cartesian math problems within quick time. We offer email based assignment help -homework help service in all math topics including Rectangular Cartesian .
Math Online Tutoring: Rectangular Cartesian
We at Expertsmind.com arrange instant online tutoring session in Rectangular Cartesian math topic. We provide latest technology based whiteboard where you can take session just like live classrooms. Math experts at expertsmind.com make clear concepts and theory in Rectangular Cartesian Math topic and provide you tricky approach to solve complex Rectangular Cartesian problems.