Parabola: The locus of a point which moves such that its distance from a fixed point is equal to its distance from a fixed straight line, i.e., e = 1 is called a parabola.
Its equation in standard form is y2 = 4 ax

(i) Focus S (a, 0)
(ii) Equation of directrix ZM is x + a = 0
(iii) Vertex is O (0, 0)
(iv) Axis of parabola is X'OX
Some definitions:
(i) Focal distance: The distance of a point on parabola from focus is called focal distance. If P(x1, y1) is on the parabola, then focal distance is x1 + a.
(ii) Focal chord: The chord of parabola which passes through focus is called focal chord of parabola.
(iii) Latus rectum: The chord of parabola which passes through focus and perpendicular to axis of parabola is called latus rectum of parabola. Its length if 4a and end points are L(a, 2a) and t'(a, - 2a).
(iv) Double ordinate: Any chord which is perpendicular to the axis of the parabola is called its double ordinate.
In the figure of parabola, PN is the ordinate of P and PNP' is the double ordinate.
Some special types of parabola:
(i) y2 = 4a (x + a) is the equation of the parabola whose focus is the origin and the axis is x-axis.
(ii) y2 = 4a (x - a) is the equation of parabola whose axis is x-axis and y-axis is directrix.
(iii) x2 = 4a (y - a) is the equation of parabola whose axis is y-axis and the directrix is x-axis.
(iv) (y - ß)2 = 4a (x - a) is the equation of parabola Whose vertex is (a, ß) and axis is parallel to x-axis.
(v) (x - a)2 = 4a (y - ß) is the equation of parabola whose vertex is (a, ß) and axis is parallel to y-axis.
(1) The equation ax2 + by2 + 2hxy + 2gx + 2ty + c = 0 will represent a parabola if h2 = ab and Δ ¹ 0.
(2) The point (x1, y1) will be outside on or within the parabola y2 = 4ax when the value of y12 - 4ax, is positive zero or negative respectively.
(3) The equation of parabola whose axis parallel to x-axis is x = Ay2 + By + C and y = Ax2 + Bx + C is a parabola with its axis parallel to y-axis.
(4) The parametric coordinates of the parabola y2 = 4ax are x = at2 and y = 2at respectively.
(5) Equation of tangent at P(x1, y1) is yy1, = 2a (x + x1) and equation of tangent in slope form is a y = mx + a/m
Here point of contact is
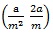
(6) Equation of normal at P (x1, y1) is y - y1

and equation of normal in slope form is
y = mx - 2am - ma3
Here foot of normal is (am2, - 2am)
(7) The line y = mx + c may be tangent to the parabola if c = a/m and may be normal to the parabola if c = - 2am - am3.
(8) Chord of contact at point (x1, y1) is yy1, = 2a (x + x1).
(9) Equation of chords joining points

(10) Points of intersection of two normal at
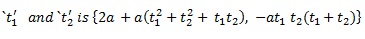
Properties of normal's:
(i) The equation of normal of the parabola is the cubic equation in m therefore, for the three values of m, three normal's can be drawn, but the tangents can be drawn maximum two on the parabola, therefore, the two values of m will be coincident, hence two normal's are coincident and one different.
(ii) The algebraic sum of gradients of normal's is zero.
(iii) The algebraic sum of ordinates of foot of normal's is zero.
(iv) The centroid of triangle formed by the joining of foot of perpendicular is on the axis of parabola.
Live Math Experts: Help with parabola Assignments - Homework
Expertsmind.com offers help with parabola assignment and homework in mathematics subject. Experts mind's mathexperts are highly qualified and experienced and they can solve your complex parabola math problems within quick time. We offer email based assignment help -homework help service in all math topics including parabola. .
Math Online Tutoring: parabola - conic sections - co-ordinate geometry
We at Expertsmind.com arrange instant online tutoring session in parabola math topic. We provide latest technology based whiteboard where you can take session just like live classrooms. Math experts at expertsmind.com make clear concepts and theory in parabola Math topic and provide you tricky approach to solve complex parabola problems.